Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T20:02:55.860Z Has data issue: false hasContentIssue false
  • English
  • Français

The asymptotic shape of the branching random walk

Published online by Cambridge University Press:  01 July 2016

J. D. Biggins
J. D. Biggins*
Affiliation:
University of Sheffield
Get access Rights & Permissions [Opens in a new window]

Abstract

In a supercritical branching random walk on Rp, a Galton–Watson process with the additional feature that people have positions, let 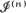be the set of positions of the nth-generation people, scaled by the factor n–1. It is shown that when the process survives 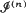looks like a convex set 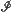for large n. An analogous result is established for an age-dependent branching process in which people also have positions. In certain cases an explicit formula for the asymptotic shape is given.

Keywords

SHAPEBRANCHING PROCESSESBRANCHING RANDOM WALK
Type
Research Article
Information
Advances in Applied Probability , Volume 10 , Issue 1 , March 1978 , pp. 62 - 84
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biggins, J. D. (1976) The first and last birth problems for a multitype age-dependent branching process. Adv. Appl. Prob. 8, 446–459.CrossRefGoogle Scholar
Biggins, J. D. (1977a) Martingale convergence in the branching random walk. J. Appl. Prob. 14, 25–37.CrossRefGoogle Scholar
Biggins, J. D. (1977b) Chernoff's Theorem in the branching random walk. J. Appl. Prob. 14,.CrossRefGoogle Scholar
Brown, L. D. (1971) Admissible estimators, recurrent diffusions and insoluble boundary value problems. Ann. Math. Statist. 42, 855–903.Google Scholar
Daniels, H. E. (1977a) Contribution to the discussion of Mollison (1977).Google Scholar
Daniels, H. E. (1977b) The advancing wave in a spatial process. J. Appl. Prob. 14 (4)Google Scholar
Hammersley, J. M. (1974) Postulates for subadditive processes. Ann. Prob. 2, 652–680.CrossRefGoogle Scholar
Harris, T. E. (1963) The Theory of Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Jagers, P. (1975) Branching Processes with Biological Applications. Wiley, London.Google Scholar
Kingman, J. F. C. (1975) The first birth problem for an age-dependent branching process. Ann. Prob. 12, 341–345.Google Scholar
Mollison, D. (1977) Spatial contact models for ecological and epidemic spread. J. R. Statist. Soc. B 39,Google Scholar
Mollison, D. (1978) Markovian contact processes. Adv. Appl. Prob. 10,CrossRefGoogle Scholar
Ney, P. E. (1965) The convergence of a random distribution function associated with a branching process. J. Math. Anal. Appl. 12, 316–327.Google Scholar
Renshaw, E. (1977) Contribution to the discussion of Mollison (1977).Google Scholar
Rockafellar, R. T. (1970) Convexity Analysis. Princeton University Press, Princeton, N.J. Google Scholar
Rogers, C. A. (1970) Hausdorff Measures. Cambridge University Press.Google Scholar