Published online by Cambridge University Press: 15 July 2020
The Gaussian polytope 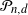 $\mathcal P_{n,d}$
is the convex hull of n independent standard normally distributed points in
$\mathcal P_{n,d}$
is the convex hull of n independent standard normally distributed points in 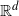 $\mathbb{R}^d$
. We derive explicit expressions for the probability that
$\mathbb{R}^d$
. We derive explicit expressions for the probability that 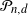 $\mathcal P_{n,d}$
contains a fixed point
$\mathcal P_{n,d}$
contains a fixed point 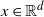 $x\in\mathbb{R}^d$
as a function of the Euclidean norm of x, and the probability that
$x\in\mathbb{R}^d$
as a function of the Euclidean norm of x, and the probability that 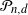 $\mathcal P_{n,d}$
contains the point
$\mathcal P_{n,d}$
contains the point 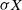 $\sigma X$
, where
$\sigma X$
, where 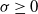 $\sigma\geq 0$
is constant and X is a standard normal vector independent of
$\sigma\geq 0$
is constant and X is a standard normal vector independent of 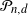 $\mathcal P_{n,d}$
. As a by-product, we also compute the expected number of k-faces and the expected volume of
$\mathcal P_{n,d}$
. As a by-product, we also compute the expected number of k-faces and the expected volume of 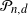 $\mathcal P_{n,d}$
, thus recovering the results of Affentranger and Schneider (Discr. and Comput. Geometry, 1992) and Efron (Biometrika, 1965), respectively. All formulas are in terms of the volumes of regular spherical simplices, which, in turn, can be expressed through the standard normal distribution function
$\mathcal P_{n,d}$
, thus recovering the results of Affentranger and Schneider (Discr. and Comput. Geometry, 1992) and Efron (Biometrika, 1965), respectively. All formulas are in terms of the volumes of regular spherical simplices, which, in turn, can be expressed through the standard normal distribution function 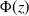 $\Phi(z)$
and its complex version
$\Phi(z)$
and its complex version 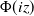 $\Phi(iz)$
. The main tool used in the proofs is the conic version of the Crofton formula.
$\Phi(iz)$
. The main tool used in the proofs is the conic version of the Crofton formula.