Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Haslett, J.
1982.
New bounds for the thermal energy storage process with stationary input.
Journal of Applied Probability,
Vol. 19,
Issue. 04,
p.
894.
Haslett, J.
1982.
New bounds for the thermal energy storage process with stationary input.
Journal of Applied Probability,
Vol. 19,
Issue. 4,
p.
894.
Hooghiemstra, G.
and
Keane, M.
1985.
Calculation of the equilibrium distribution for a solar energy storage model.
Journal of Applied Probability,
Vol. 22,
Issue. 04,
p.
852.
Hooghiemstra, G.
and
Scheffer, C.L.
1986.
Some limit theorems for an energy storage model.
Stochastic Processes and their Applications,
Vol. 22,
Issue. 1,
p.
121.
de Haan, L.
1986.
A STOCHASTIC PROCESS THAT IS AUTOREGRESSIVE IN TWO DIRECTIONS OF TIME..
Statistica Neerlandica,
Vol. 40,
Issue. 1,
p.
39.
Davis, Richard A.
and
Resnick, Sidney I.
1989.
Basic properties and prediction of max-ARMA processes.
Advances in Applied Probability,
Vol. 21,
Issue. 4,
p.
781.
Alpuim, M. T.
and
Athayde, E.
1990.
On the stationary distribution of some extremal Markovian sequences.
Journal of Applied Probability,
Vol. 27,
Issue. 02,
p.
291.
den Hollander, F.
Hooghiemstra, G.
Keane, M.
and
Resing, J.
1991.
Strong law and central limit theorem for a process between maxima and sums.
Probability Theory and Related Fields,
Vol. 90,
Issue. 1,
p.
37.
Greenwood, Priscilla E.
and
Hooghiemstra, Gerard
1991.
On the domain of attraction of an operator between supremum and sum.
Probability Theory and Related Fields,
Vol. 89,
Issue. 2,
p.
201.
Jaouhari, Salama
1994.
On the stationary law of a nonlinear autoregressive Markov chain.
Stochastic Processes and their Applications,
Vol. 51,
Issue. 2,
p.
341.
Glasserman, Paul
and
Yao, David D.
1995.
Stochastic vector difference equations with stationary coefficients.
Journal of Applied Probability,
Vol. 32,
Issue. 04,
p.
851.
Alpuim, M.T.
Catkan, N.A.
and
Hüsler, J.
1995.
Extremes and clustering of nonstationary max-AR(1) sequences.
Stochastic Processes and their Applications,
Vol. 56,
Issue. 1,
p.
171.
Лебедев, Алексей Викторович
and
Lebedev, Alexey Viktorovich
2008.
Статистический анализ MARMA-процессов первого порядка.
Математические заметки,
Vol. 83,
Issue. 4,
p.
552.
Lebedev, A. V.
2008.
Statistical analysis of first-order MARMA processes.
Mathematical Notes,
Vol. 83,
Issue. 3-4,
p.
506.
Феррейра, Марта
and
Ferreira, Marta
2011.
О зависимости от поведения хвостов: описание характера процессов максимум-авторегрессии первого порядка.
Математические заметки,
Vol. 90,
Issue. 6,
p.
902.
Ferreira, M.
2011.
On tail dependence: A characterization for first-order max-autoregressive processes.
Mathematical Notes,
Vol. 90,
Issue. 5-6,
p.
882.
Ferreira, Marta
and
Ferreira, Helena
2013.
Extremes of multivariate ARMAX processes.
TEST,
Vol. 22,
Issue. 4,
p.
606.
Scotto, Manuel G.
Weiß, Christian H.
Möller, Tobias A.
and
Gouveia, Sónia
2018.
The max-INAR(1) model for count processes.
TEST,
Vol. 27,
Issue. 4,
p.
850.
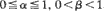 , 0<β <1, can be regarded as a simple thermal energy storage model with controlled input. Attention is mostly confined to the study of μ = EX where the random variable X has the stationary distribution for {Xn}. Even for special cases such as i.i.d. Yn or α = 0, little explicit information appears to be available on the distribution of X or μ . Accordingly, bounding techniques that have been exploited in queueing theory are used to study μ . The various bounds are illustrated numerically in a range of special cases.
, 0<β <1, can be regarded as a simple thermal energy storage model with controlled input. Attention is mostly confined to the study of μ = EX where the random variable X has the stationary distribution for {Xn}. Even for special cases such as i.i.d. Yn or α = 0, little explicit information appears to be available on the distribution of X or μ . Accordingly, bounding techniques that have been exploited in queueing theory are used to study μ . The various bounds are illustrated numerically in a range of special cases.

