Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T12:19:02.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Sub-tree counts on hyperbolic random geometric graphs

Part of: Limit theorems Real and complex geometry Graph theory Geometric probability and stochastic geometry

Published online by Cambridge University Press:  13 June 2022

Takashi Owada  and
D. Yogeshwaran Open the ORCID record for D. Yogeshwaran [Opens in a new window]
Takashi Owada*
Affiliation:
Purdue University
D. Yogeshwaran*
Affiliation:
Indian Statistical Institute
*
*Postal address: Department of Statistics, Purdue University, West Lafayette, IN 47907, USA. Email address: [email protected]
**Postal address: Theoretical Statistics and Mathematics Unit, Indian Statistical Institute, 8th Mile, Mysore Road, Bangalore, 560059, INDIA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The hyperbolic random geometric graph was introduced by Krioukov et al. (Phys. Rev. E82, 2010). Among many equivalent models for the hyperbolic space, we study the d-dimensional Poincaré ball (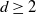 $d\ge 2$ ), with a general connectivity radius. While many phase transitions are known for the expectation asymptotics of certain subgraph counts, very little is known about the second-order results. Two of the distinguishing characteristics of geometric graphs on the hyperbolic space are the presence of tree-like hierarchical structures and the power-law behaviour of the degree distribution. We aim to reveal such characteristics in detail by investigating the behaviour of sub-tree counts. We show multiple phase transitions for expectation and variance in the resulting hyperbolic geometric graph. In particular, the expectation and variance of the sub-tree counts exhibit an intricate dependence on the degree sequence of the tree under consideration. Additionally, unlike the thermodynamic regime of the Euclidean random geometric graph, the expectation and variance may exhibit different growth rates, which is indicative of power-law behaviour. Finally, we also prove a normal approximation for sub-tree counts using the Malliavin–Stein method of Last et al. (Prob. Theory Relat. Fields165, 2016), along with the Palm calculus for Poisson point processes.

Keywords

Hyperbolic spacesrandom geometric graphsPoisson point processsub-tree countscentral limit theoremMalliavin–Stein method

MSC classification

Primary: 60F05: Central limit and other weak theorems 60D05: Geometric probability and stochastic geometry
Secondary: 05C80: Random graphs 51M10: Hyperbolic and elliptic geometries (general) and generalizations
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 4 , December 2022 , pp. 1032 - 1069
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullah, M. A., Bode, M. and Fountoulakis, N. (2017). Typical distances in a geometric model for complex networks. Internet Math. 1.CrossRefGoogle Scholar
Anderson, J. W. (2008). Hyperbolic Geometry, 2nd edn. Springer, London.Google Scholar
Baccelli, F. and Blaszczyszyn, B. (2009). Stochastic Geometry and Wireless Networks, Vol. I, Theory. Now Publishers, Boston.Google Scholar
Baccelli, F. and Blaszczyszyn, B. (2010). Stochastic Geometry and Wireless Networks, Vol. II, Applications. Now Publishers, Boston.Google Scholar
Benjamini, I. (2013). Coarse Geometry and Randomness: école d’été de Probabilités de Saint-Flour XLI—2011. Springer, Cham.CrossRefGoogle Scholar
Benjamini, I. and Schramm, O. (2001). Percolation in the hyperbolic plane. J. Amer. Math. Soc. 4, 487–507.Google Scholar
Bläsius, T., Friedrich, T. and Krohmer, A. (2018). Cliques in hyperbolic random graphs. Algorithmica 80, 2324–2344.CrossRefGoogle Scholar
Bobrowski, O. and Mukherjee, S. (2015). The topology of probability distributions on manifolds. Prob. Theory Relat. Fields 161, 651–686.CrossRefGoogle Scholar
Bobrowski, O. and Oliveira, G. (2019). Random Čech complexes on Riemannian manifolds. Random Structures Algorithms 54, 373–412.CrossRefGoogle Scholar
Bode, M., Fountoulakis, N. and Müller, T. (2015). On the largest component of a hyperbolic model of complex networks. Electron. J. Combinatorics 22, 3–24.CrossRefGoogle Scholar
Bode, M., Fountoulakis, N. and Müller, T. (2016). The probability of connectivity in a hyperbolic model of complex networks. Random Structures Algorithms 49, 65–94.CrossRefGoogle Scholar
Brooks, R. and Makover, E. (2004). Random construction of Riemann surfaces. J. Differential Geom. 68, 121–157.CrossRefGoogle Scholar
Candellero, E. and Fountoulakis, N. (2016). Bootstrap percolation and the geometry of complex networks. Stoch. Process. Appl. 126, 234–264.CrossRefGoogle Scholar
Candellero, E. and Fountoulakis, N. (2016). Clustering and the hyperbolic geometry of complex networks. Internet Math. 12, 2–53.CrossRefGoogle Scholar
Cannon, J. W., Floyd, W. J., Kenyon, R. and Parry, W. R. (1997). Hyperbolic geometry. In Flavors of Geometry, ed. Levy, S., Cambridge University Press, pp. 59–115.Google Scholar
Castellanos, J. A. J. and Darnell, E. (2007). NonEuclid 2007.04. Available at http://cs.unm.edu/ joel/NonEuclid/NonEuclid.html.Google Scholar
Cunningham, W., Zuev, K. and Krioukov, D. (2017). Navigability of random geometric graphs in the universe and other spacetimes. Sci. Reports 7, paper no. 8699.Google Scholar
De Kergorlay, H. L., Tillmann, U. and Vipond, O. (2019). Random Čech complexes on manifolds with boundary. To appear in Random Structures Algorithms.Google Scholar
Fountoulakis, N. (2012). On the evolution of random graphs on spaces of negative curvature. Preprint. Available at https://arxiv.org/abs/1205.2923.Google Scholar
Fountoulakis, N. (2015). On a geometrization of the Chung–Lu model for complex networks. J. Complex Networks 3, 361–387.CrossRefGoogle Scholar
Fountoulakis, N., van der Hoorn, P., Müller, T. and Schepers, M. (2021). Clustering in a hyperbolic model of complex networks. Electron. J. Prob. 26, 132 pp.CrossRefGoogle Scholar
Fountoulakis, N. and Müller, T. (2018). Law of large numbers for the largest component in a hyperbolic model of complex networks. Ann. Appl. Prob. 28, 607–650.CrossRefGoogle Scholar
Fountoulakis, N. and Yukich, J. (2020). Limit theory for isolated and extreme points in hyperbolic random geometric graphs. Electron. J. Prob. 25, 51 pp.CrossRefGoogle Scholar
Gilbert, E. N. (1961). Random plane networks. J. SIAM 9, 533–543.Google Scholar
Gugelmann, L., Panagiotou, K. and Peter, U. (2012). Random hyperbolic graphs: degree sequence and clustering. In Automata, Languages, and Programming, Springer, Berlin, Heidelberg, pp. 573–585.CrossRefGoogle Scholar
Haenggi, M. (2012). Stochastic Geometry for Wireless Networks. Cambridge University Press.CrossRefGoogle Scholar
Kiwi, M. and Mitsche, D. (2014). A bound for the diameter of random hyperbolic graphs. In 2015 Proceedings of the Twelfth Workshop on Analytic Algorithmics and Combinatorics (ANALCO), Society for Industrial and Applied Mathematics, Philadelphia, pp. 26–39.Google Scholar
Kiwi, M. and Mitsche, D. (2018). Spectral gap of random hyperbolic graphs and related parameters. Ann. Appl. Prob. 28, 941–989.CrossRefGoogle Scholar
Kiwi, M. and Mitsche, D. (2019). On the second largest component of random hyperbolic graphs. SIAM J. Discrete Math. 33, 2200–2217.CrossRefGoogle Scholar
Krioukov, D. et al. (2010). Hyperbolic geometry of complex networks. Phys. Rev. E 82, paper no. 036106.CrossRefGoogle Scholar
Lalley, S. P. (2014). Statistical regularities of self-intersection counts for geodesics on negatively curved surfaces. Duke Math. J. 163, 1191–1261.CrossRefGoogle Scholar
Last, G., Peccati, G. and Schulte, M. (2016). Normal approximation on Poisson spaces: Mehler’s formula, second order Poincaré inequalities and stabilization. Prob. Theory Relat. Fields 165, 667–723.CrossRefGoogle Scholar
Last, G. and Penrose, M. (2017). Lectures on the Poisson Process. Cambridge University Press.CrossRefGoogle Scholar
Lyons, R. and Peres, Y. (2016). Probability on Trees and Networks. Cambridge University Press.CrossRefGoogle Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. Cambridge University Press.CrossRefGoogle Scholar
Müller, T. and Staps, M. (2019). The diameter of KPKVB random graphs. Adv. Appl. Prob. 51, 358–377.CrossRefGoogle Scholar
Peccati, G. and Reitzner, M. (eds) (2016). Stochastic Analysis for Poisson Point Processes: Malliavin Calculus, Wiener–Itô Chaos Expansions and Stochastic Geometry. Springer, Cham.CrossRefGoogle Scholar
Penrose, M. (2003). Random Geometric Graphs. Oxford University Press.CrossRefGoogle Scholar
Penrose, M. D. and Yukich, J. E. (2013). Limit theory for point processes in manifolds. Ann. Appl. Prob. 23, 2161–2211.CrossRefGoogle Scholar
Petri, B. and Thaele, C. (2018). Poisson approximation of the length spectrum of random surfaces. Indiana Univ. Math. J. 67, 1115–1141.CrossRefGoogle Scholar
Ratcliffe, J. G. (2006). Foundations of Hyperbolic Manifolds. Springer, New York.Google Scholar
Yukich, J. E. (2006). Probability Theory of Classical Euclidean Optimization Problems. Springer, Berlin, Heidelberg.Google Scholar