Published online by Cambridge University Press: 13 June 2022
Let 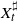 $X_t^\sharp$
be a multivariate process of the form
$X_t^\sharp$
be a multivariate process of the form 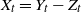 $X_t =Y_t - Z_t$
,
$X_t =Y_t - Z_t$
, 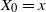 $X_0=x$
, killed at some terminal time T, where
$X_0=x$
, killed at some terminal time T, where 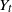 $Y_t$
is a Markov process having only jumps of length smaller than
$Y_t$
is a Markov process having only jumps of length smaller than 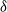 $\delta$
, and
$\delta$
, and 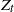 $Z_t$
is a compound Poisson process with jumps of length bigger than
$Z_t$
is a compound Poisson process with jumps of length bigger than 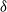 $\delta$
, for some fixed
$\delta$
, for some fixed 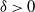 $\delta>0$
. Under the assumptions that the summands in
$\delta>0$
. Under the assumptions that the summands in 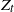 $Z_t$
are subexponential, we investigate the asymptotic behaviour of the potential function
$Z_t$
are subexponential, we investigate the asymptotic behaviour of the potential function 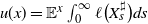 $u(x)= \mathbb{E}^x \int_0^\infty \ell\big(X_s^\sharp\big)ds$
. The case of heavy-tailed entries in
$u(x)= \mathbb{E}^x \int_0^\infty \ell\big(X_s^\sharp\big)ds$
. The case of heavy-tailed entries in 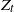 $Z_t$
corresponds to the case of ‘big claims’ in insurance models and is of practical interest. The main approach is based on the fact that u(x) satisfies a certain renewal equation.
$Z_t$
corresponds to the case of ‘big claims’ in insurance models and is of practical interest. The main approach is based on the fact that u(x) satisfies a certain renewal equation.