Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T07:38:45.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Orders Generated by Integrals: a Unified Study

Part of: Distribution theory - Probability Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  01 July 2016

Alfred Müller
Alfred Müller*
Affiliation:
Universität Karlsruhe
*
∗ Postal address: Institut für Wirtschaftstheorie und Operations Research, Universität Karlsruhe, Kaiserstr. 12, D-76128 Karlsruhe, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

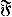We consider stochastic orders of the following type. Let be a class of functions and let P and Q be probability measures. Then define 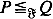, if ∫ ⨍ d P ≦ ∫ ⨍ d Q for all f in 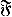. Marshall (1991) posed the problem of characterizing the maximal cone of functions generating such an ordering. We solve this problem by using methods from functional analysis. Another purpose of this paper is to derive properties of such integral stochastic orders from conditions satisfied by the generating class of functions. The results are illustrated by several examples. Moreover, we show that the likelihood ratio order is closed with respect to weak convergence, though it is not generated by integrals.

Keywords

INTEGRAL STOCHASTIC ORDERSCLOSURE PROPERTIESMAXIMAL GENERATORLIKELIHOOD RATIO ORDER

MSC classification

Primary: 60E15: Inequalities; stochastic orderings
Secondary: 60B11: Probability theory on linear topological spaces 60E05: Distributions
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 2 , June 1997 , pp. 414 - 428
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Choquet, G. (1969) Lectures on Analysis II. Benjamin, New York.Google Scholar
Dudley, R. M. (1989) Real Analysis and Probability. Wadsworth and Brooks, Belmont, CA.Google Scholar
Kamae, T., Krengel, U. and O'Brien, G. L. (1977) Stochastic inequalities on partially ordered spaces. Ann. Prob. 5, 899–912.CrossRefGoogle Scholar
Karlin, S. and Rinott, Y. (1980) Classes of orderings of measures and related correlation inequalities. J. Multivar. Anal. 10, 467–498.CrossRefGoogle Scholar
Lehmann, E. (1955), Ordered families of distributions. Ann. Math. Statist. 26, 399–419.CrossRefGoogle Scholar
Marshall, A. W. (1991) Multivariate stochastic orderings and generating cones of functions. In Stochastic Orders and Decision Under Risk. (IMS Lecture Notes-Monograph Series 19.) ed. Mosler, K. and Scarsini, M. IMS, New York. pp. 231–247.CrossRefGoogle Scholar
Mosler, K. and Scarsini, M. (1991) Some theory of stochastic dominance. In Stochastic Orders and Decision Under Risk. (IMS Lecture Notes-Monograph Series 19.) ed. Mosler, K. and Scarsini, M. IMS, New York. pp. 261–284.CrossRefGoogle Scholar
Mosler, K. and Scarsini, M. (1994) Stochastic Orders and Applications: A Classified Bibliography. (Lecture Notes in Econ. Math. Syst. 401.) CrossRefGoogle Scholar
Nachbin, L. (1965) Topology and Order. (Van Nostrand Math. Studies 4.) Van Nostrand, Princeton, NJ.Google Scholar
Reuter, H. and Riedrich, T. (1981) On maximal sets of functions compatible with a partial ordering for distribution functions. Math. Operations forsch. Statist. 12, 597–605.Google Scholar
Shared, M. and Shanthikumar, J. G. (1994) Stochastic Orders and their Applications. Academic Press, London.Google Scholar
Shanthikumar, J. G. and Yao, D. D. (1986). The preservation of likelihood ratio ordering under convolution. Stoch. Proc. Appl. 23, 259–267.CrossRefGoogle Scholar
Stoyan, D. (1983) Comparison Methods for Queues and Other Stochastic Models. Wiley, Chichester.Google Scholar
Szekli, R. (1995) Stochastic Ordering and Dependence in Applied Probability. (Lecture Notes in Statistics 97.) Springer, New York.CrossRefGoogle Scholar
Szekli, R., Disney, R. L. and Hur, S. (1994) MR/GI/1 queues with positively correlated arrival streams. J. Appl. Prob. 31, 497–514.CrossRefGoogle Scholar
Wheeden, R. L. and Zygmund, A. (1977) Measure and Integral. Dekker, New York.CrossRefGoogle Scholar
Whitt, W. (1986) Stochastic comparisons for non-Markov processes. Math. Operat. Res. 11, 608–618.CrossRefGoogle Scholar