Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T21:16:08.692Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic Analysis of ‘Simultaneous Merge–Sort'

Part of: Computer aspects of numerical algorithms Limit theorems

Published online by Cambridge University Press:  01 July 2016

M. Cramer
M. Cramer*
Affiliation:
University of Freiburg
Get access Rights & Permissions [Opens in a new window]

Abstract

The asymptotic behaviour of the recursion 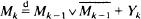is investigated; Yk describes the number of comparisons which have to be carried out to merge two sorted subsequences of length 2k–1 and Mk can be interpreted as the number of comparisons of ‘Simultaneous Merge–Sort'. The challenging problem in the analysis of the above recursion lies in the fact that it contains a maximum as well as a sum. This demands different ideal properties for the metric in the contraction method. By use of the weighted Kolmogorov metric it is shown that an exponential normalization provides the recursion's convergence. Furthermore, one can show that any sequence of linear normalizations of Mk must converge towards a constant if it converges in distribution at all.

Keywords

ALGORITHMSTOCHASTIC RECURSIONLIMIT THEOREMSPROBABILITY METRICS

MSC classification

Primary: 65Y20: Complexity and performance of numerical algorithms
Secondary: 60F05: Central limit and other weak theorems
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 3 , September 1997 , pp. 669 - 694
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Knuth, D. E. (1973) The Art of Computer Programming. Vol. 3: Sorting and Searching. Addison-Wesley, Reading, MA Google Scholar
Rachev, S. T. (1991) Probability Metrics and the Stability of Stochastic Models. Wiley, New York.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1995) Probability metrics and recursive algorithms. Adv. Appl. Prob. 27, 770–799.Google Scholar