Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T14:54:11.557Z Has data issue: false hasContentIssue false
  • English
  • Français

Solving the inverse problem for measures using iterated function systems: a new approach

Part of: Classical measure theory General theory of differentiable manifolds Approximations and expansions

Published online by Cambridge University Press:  01 July 2016

B. Forte  and
E. R. Vrscay
B. Forte*
Affiliation:
University of Waterloo
E. R. Vrscay*
Affiliation:
University of Waterloo
*
* Present address: Facoltà di Scienze MM. FF. e NN. a Càvignal, Università degli Studi di Verona, Strada Le Grazie, 37134 Verona, Italy.
** Postal address: Department of Applied Mathematics, Faculty of Mathematics, University of Waterloo, Waterloo, Ontario, Canada N2L 3G1.
Get access Rights & Permissions [Opens in a new window]

Abstract

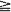We present a systematic method of approximating, to an arbitrary accuracy, a probability measure µ on x = [0,1]q, q 1, with invariant measures for iterated function systems by matching its moments. There are two novel features in our treatment. 1. An infinite set of fixed affine contraction maps on 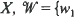, w2, · ·· }, subject to an ‘ϵ-contractivity' condition, is employed. Thus, only an optimization over the associated probabilities pi is required. 2. We prove a collage theorem for moments which reduces the moment matching problem to that of minimizing the collage distance between moment vectors. The minimization procedure is a standard quadratic programming problem in the pi which can be solved in a finite number of steps. Some numerical calculations for the approximation of measures on [0, 1] are presented.

Keywords

COLLAGE DISTANCEQUADRATIC PROGRAMMINGDATA COMPRESSION

MSC classification

Primary: 28A80: Fractals
Secondary: 41A20: Approximation by rational functions 58A40: Differential spaces
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 27 , Issue 3 , September 1995 , pp. 800 - 820
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Abenda, S., Demko, S. and Turchetti, G. (1992) Local moments and inverse problem for fractal measures. Inverse Problems 8, 737–750.Google Scholar
[2] Abenda, S. and Turchetti, G. (1989) Inverse problem of fractal sets on the real line via the moment method. Nuovo Cim. 104B, 213–227.CrossRefGoogle Scholar
[3] Akhiezer, N. I. (1965) The Classical Moment Problem and Some Related Questions in Analysis. Hafner, New York.Google Scholar
[4] Barnsley, M. F. (1988) Fractals Everywhere. Academic Press, New York.Google Scholar
[5] Barnsley, M. F. and Demko, S. (1985) Iterated function systems and the global construction of fractals. Proc. R. Soc. London A399, 243–275.Google Scholar
[6] Barnsley, M. F. and Elton, J. H. (1988) A new class of Markov processes for image encoding. Adv. Appl. Prob. 20, 14–32.Google Scholar
[7] Barnsley, M. F., Hardin, D., Ervin, V. and Lancaster, J. (1986) Solution of an inverse problem for fractals and other sets. Proc. Nat. Acad. Sci. USA 83, 1975–1977.CrossRefGoogle ScholarPubMed
[8] Bessis, D. and Demko, S. (1991) Stable recovery of fractal measures by polynomial sampling. Physica 47D, 427.Google Scholar
[9] Best, J. J. and Ritter, K. (1988) A quadratic programming algorithm. Z. Operat. Res. 32, 271–297.Google Scholar
[10] Cabrelli, C. A., Molter, U. M. and Vrscay, E. R. (1992) “Moment matching” for the approximation of measures using iterated function systems. Preprint.Google Scholar
[11] Cabrelli, C. A., Forte, B., Molter, U. M. and Vrscay, E. R. (1992) Iterated fuzzy set systems: A new approach to the inverse problem for fractals and other sets. J. Math. Anal. Appl. 171, 79–100.Google Scholar
[12] Centore, P. and Vrscay, E. R. (1994) Continuity of attractors and invariant measures for iterated function systems. Canad. Math. Bull. 37, 315–329.Google Scholar
[13] Diaconis, P. and Shahshahani, M. (1986) Products of random matrices and computer image generation. Contemp. Math. 50, 173–182.Google Scholar
[14] Elton, J. and Yan, Z. (1989) Approximation of measures by Markov processes and homogeneous affine iterated function systems. Constr. Approx. 5, 69–87.Google Scholar
[15] Forte, B., Lo Schiavo, M. and Vrscay, E. R. (1994) Continuity properties of attractors for iterated fuzzy set systems. J. Austral. Math. Soc. B 36, 175–193.Google Scholar
[16] Forte, B. and Vrscay, E. R. (1995) Solving the inverse problem for function and image approximation using iterated function systems. Dynamics of Continuous, Discrete and Impulsive Systems. To appear.CrossRefGoogle Scholar
[17] Forte, B. and Vrscay, E. R. (1994) Solving the inverse problem for function and image approximation using iterated function systems I. Theoretical basis. Fractals 2, 325–334. II. Algorithm and computations. Fractals 2, 335-346.Google Scholar
[18] Handy, C. and Mantica, G. (1990) Inverse problems in fractal construction: moment method solution. Physica D43, 17–36.Google Scholar
[19] Hutchinson, J. (1981) Fractals and self-similarity. Indiana Univ. J. Math 30, 713–747.CrossRefGoogle Scholar
[20] Isenberg, C. (1963) Moment calculations in lattice dynamics, I. FCC lattice with nearest-neighbour interactions. Phys. Rev. 132, 2427–2433.Google Scholar
[21] Jacquin, A. (1989) A Fractal Theory of Iterated Markov Operators with Applications to Digital Image Coding. Ph.D. Thesis, Georgia Institute of Technology.Google Scholar
[22] Mantica, G. and Sloan, A. (1989) Chaotic optimization and the construction of fractals: solution of an inverse problem. Complex Systems 3, 37–62.Google Scholar
[23] Parthasarathy, K. R. (1967) Probability Measures on Metric Spaces. Academic Press, New York.Google Scholar
[24] Vrscay, E. R. (1991) Moment and collage methods for the inverse problem of fractal construction with iterated function systems. In Fractals in the Fundamental and Applied Sciences, ed. by Peitgen, H.-O., Henriques, J. M. and Penedo, L. F., pp. 443–461. North-Holland, Amsterdam.Google Scholar
[25] Vrscay, E. R. (1991) Iterated function systems: theory, applications and the inverse problem. In Proceedings of the NATO Advanced Study Institute on Fractal Geometry and Analysis, ed. Belair, J. and Dubuc, S., pp. 405–468. Kluwer, Dordrecht.CrossRefGoogle Scholar
[26] Vrscay, E. R. and Roehrig, C. (1989) Iterated function systems and the inverse problem of fractal construction using moments. In Computers and Mathematics, ed. Kaltofen, E. and Watt, S. M., pp. 250–259. Springer-Verlag, New York.Google Scholar
[27] Wheeler, J. C. and Gordon, R. G. (1970) Bounds for averages using moment constraints. In The Padé Approximant in Theoretical Physics, ed. Baker, G. A. Jr and Gammel, J. L., pp. 99–128. Academic Press, New York.CrossRefGoogle Scholar