Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rootzén, Holger
1984.
Statistical Extremes and Applications.
p.
167.
Berman, Simeon M.
1986.
The supremum of a process with stationary independent and symmetric increments.
Stochastic Processes and their Applications,
Vol. 23,
Issue. 2,
p.
281.
Imhof, J.-P.
1986.
On the time spent above a level by Brownian motion with negative drift.
Advances in Applied Probability,
Vol. 18,
Issue. 4,
p.
1017.
Wilson, Richard J.
1988.
Model fields in crossing theory: a weak convergence perspective.
Advances in Applied Probability,
Vol. 20,
Issue. 4,
p.
756.
Doney, R. A.
and
Grey, D. R.
1989.
Some remarks on Brownian motion with drift.
Journal of Applied Probability,
Vol. 26,
Issue. 3,
p.
659.
Simeon, M.Berman
1993.
A central limit theorem for extreme sojourns of diffusion processes.
Stochastic Analysis and Applications,
Vol. 11,
Issue. 4,
p.
399.
Albin, J.M.P.
1993.
Extremes of diffusions over fixed intervals.
Stochastic Processes and their Applications,
Vol. 48,
Issue. 2,
p.
211.
Klass, Michael
and
Pitman, Jim
1993.
Limit laws for Brownian motion conditioned to reach a high level.
Statistics & Probability Letters,
Vol. 17,
Issue. 1,
p.
13.
Doney, R. A.
1993.
Some results involving the maximum of Brownian motion.
Journal of Applied Probability,
Vol. 30,
Issue. 4,
p.
805.
Cline, D.B.H.
and
Samorodnitsky, G.
1994.
Subexponentiality of the product of independent random variables.
Stochastic Processes and their Applications,
Vol. 49,
Issue. 1,
p.
75.
Berman, S. M.
1994.
A class of laplace transforms arising in a diffusion problem.
Communications on Pure and Applied Mathematics,
Vol. 47,
Issue. 1,
p.
93.
Louchard, G.
Kenyon, Claire
and
Schott, R.
1997.
Data Structures' Maxima.
SIAM Journal on Computing,
Vol. 26,
Issue. 4,
p.
1006.
Djurčić, Dragan
and
Torgašev, Aleksandar
2001.
Strong Asymptotic Equivalence and Inversion of Functions in the Class Kc.
Journal of Mathematical Analysis and Applications,
Vol. 255,
Issue. 2,
p.
383.
Buldygin, V. V.
Klesov, O. I.
and
Steinebach, J. G.
2007.
PRV property and the ϕ-asymptotic behavior of solutions of stochastic differential equations.
Lithuanian Mathematical Journal,
Vol. 47,
Issue. 4,
p.
361.
Wang, Shijie
and
Wang, Wensheng
2007.
Precise Large Deviations for Sums of Random Variables with Consistently Varying Tails in Multi-Risk Models.
Journal of Applied Probability,
Vol. 44,
Issue. 4,
p.
889.
Djurčić, D.
Torgašev, A.
and
Ješić, S.
2008.
The strong asymptotic equivalence and the generalized inverse.
Siberian Mathematical Journal,
Vol. 49,
Issue. 4,
p.
628.
Djurčić, Dragan
Torgašev, Aleksandar
and
Clark, Stephen
2009.
A Theorem of Galambos‐Bojanić‐Seneta Type.
Abstract and Applied Analysis,
Vol. 2009,
Issue. 1,
Buldygin, Valeriĭ V.
Indlekofer, Karl-Heinz
Klesov, Oleg I.
and
Steinebach, Josef G.
2018.
Pseudo-Regularly Varying Functions and Generalized Renewal Processes.
Vol. 91,
Issue. ,
p.
53.
Buldygin, Valeriĭ V.
Indlekofer, Karl-Heinz
Klesov, Oleg I.
and
Steinebach, Josef G.
2018.
Pseudo-Regularly Varying Functions and Generalized Renewal Processes.
Vol. 91,
Issue. ,
p.
311.
Klesov, O.I.
and
Steinebach, J.G.
2020.
On preserving the limit points of corresponding objects.
Journal of Mathematical Analysis and Applications,
Vol. 486,
Issue. 2,
p.
123916.


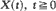 , be an Ito diffusion process on the real line. For
, be an Ito diffusion process on the real line. For 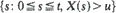 . Limit theorems are obtained for (i) the distribution of
. Limit theorems are obtained for (i) the distribution of 