Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-07T20:56:46.068Z Has data issue: false hasContentIssue false
  • English
  • Français

Smallest-fit selection of random sizes under a sum constraint: weak convergence and moment comparisons

Part of: Limit theorems Operations research and management science Stochastic processes

Published online by Cambridge University Press:  01 July 2016

Frans A. Boshuizen  and
Robert P. Kertz
Frans A. Boshuizen*
Affiliation:
ING Bank Amsterdam
Robert P. Kertz*
Affiliation:
Georgia Institute of Technology
*
∗ Postal address: ING Bank Amsterdam, The Netherlands.
∗∗ Postal address: School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332-0160, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, in work strongly related with that of Coffman et al. [5], Bruss and Robertson [2], and Rhee and Talagrand [15], we focus our interest on an asymptotic distributional comparison between numbers of ‘smallest’ i.i.d. random variables selected by either on-line or off-line policies. Let X1,X2,… be a sequence of i.i.d. random variables with distribution function F(x), and let X1,n,…,Xn,n be the sequence of order statistics of X1,…,Xn. For a sequence (cn)n≥1 of positive constants, the smallest fit off-line counting random variable is defined by Ne(cn) := max {j ≤ n : X1,n + … + Xj,n ≤ cn}. The asymptotic joint distributional comparison is given between the off-line count Ne(cn) and on-line counts Nnτ for ‘good’ sequential (on-line) policies τ satisfying the sum constraint ∑j≥1XτjI(τj≤n) ≤ cn. Specifically, for such policies τ, under appropriate conditions on the distribution function F(x) and the constants (cn)n≥1, we find sequences of positive constants (Bn)n≥1, (Δn)n≥1 and (Δ'n)n≥1 such that

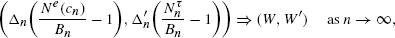
for some non-degenerate random variables W and W'. The major tools used in the paper are convergence of point processes to Poisson random measure and continuous mapping theorems, strong approximation results of the normalized empirical process by Brownian bridges, and some renewal theory.

Keywords

Joint convergence in distributionextreme sumsorder statisticsthreshold strategiescounting r.v.sPoisson random measurescontinuous mapping principlestrong approximationsBrownian bridgeon-line vs off-line strategies

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory 60G70: Extreme value theory; extremal processes
Secondary: 60F05: Central limit and other weak theorems 60F15: Strong theorems 60G55: Point processes 90B50: Management decision making, including multiple objectives
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 31 , Issue 1 , March 1999 , pp. 178 - 198
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1968). Convergence of Probability Measures. Wiley, New York.Google Scholar
Bruss, F. T. and Robertson, J. B. (1991). ‘Wald's lemma’ for sums of order statistics of i.i.d. random variables. Adv. Appl. Prob. 23, 612–623.Google Scholar
Chow, Y. S. and Teicher, H. (1978). Probability Theory: Independence, Interchangeability, Martingales. Springer, New York.CrossRefGoogle Scholar
Chung, K. L. (1974). A Course in Probability Theory, 2nd edn. Academic Press, New York.Google Scholar
Coffman, E. G., Flatto, L. and Weber, R. R. (1987). Optimal selection of stochastic intervals under a sum constraint. Adv. Appl. Prob. 19, 454–473.CrossRefGoogle Scholar
Csörgő, M., Csörgő, S., Horváth, L. and Mason, D. M. (1986). Weighted empirical and quantile processes. Ann. Prob. 14, 31–85.CrossRefGoogle Scholar
Csörgő, M., Csörgő, S. and Horváth, L. (1986). An Asymptotic Theory for Empirical Reliability and Concentration Processes (Lecture Notes in Stat. 33). Springer, Berlin.Google Scholar
Csörgő, S. and Mason, D. M. (1986). The asymptotic distribution of sums of extreme values from a regularly varying distribution. Ann. Prob. 14, 974–983.Google Scholar
Csörgő, S., Horváth, L. and Mason, D. M. (1986). What portion of the sample makes a partial sum asymptotically stable or normal? Prob. Theory Rel. Fields 72, 1–16.CrossRefGoogle Scholar
Csörgő, S., Haeusler, E. and Mason, D. (1991). The asymptotic distribution of extreme sums. Ann. Prob. 19, 783–811.CrossRefGoogle Scholar
Gut, A. (1988). Stopped Random Walks: Limit Theorems and Applications. Springer, New York.Google Scholar
Kennedy, D. P. and Kertz, R. P. (1990). Limit theorems for threshold-stopped random variables with applications to optimal stopping. Adv. Appl. Prob. 22, 396–411.Google Scholar
Lo, G. S. (1989). A note on the asymptotic normality of extreme values. J. Statist. Planning Inference 22, 127–136.Google Scholar
Resnick, S. (1987). Extreme Values, Regular Variation, and Point Processes. Springer, New York.Google Scholar
Rhee, W. and Talagrand, M. (1991). A note on the selection of random variables under a sum constraint. J. Appl. Prob. 28, 919–923.CrossRefGoogle Scholar
Whitt, W. (1980). Some useful functions for functional limit theorems. Math. Operat. Res. 5, 67–85.Google Scholar