Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T16:03:45.481Z Has data issue: false hasContentIssue false
  • English
  • Français

The sharp threshold for jigsaw percolation in random graphs

Part of: Graph theory Combinatorial probability Special processes

Published online by Cambridge University Press:  07 August 2019

Oliver Cooley ,
Tobias Kapetanopoulos  and
Tamás Makai
Oliver Cooley*
Affiliation:
Graz University of Technology
Tobias Kapetanopoulos*
Affiliation:
Goethe University Frankfurt
Tamás Makai*
Affiliation:
Queen Mary University of London
*
*Postal address: Institute of Discrete Mathematics, Graz University of Technology, Steyrergasse 30, 8010 Graz, Austria. Email address: [email protected] Supported by the Austrian Science Fund (FWF) & German Research Foundation (DFG) under grant I3747.
**Postal address: Mathematics Institute, Goethe University, 10 Robert Mayer Street, Frankfurt 60325, Germany. Email address: [email protected] Supported by a Stiftung Polytechnische Gesellschaft PhD grant.
***Postal address: School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS. Email address: [email protected] Supported by the Austrian Science Fund (FWF) under grant P26826 and the EPSRC under grant EP/N004221/1.
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the jigsaw percolation process, which may be seen as a measure of whether two graphs on the same vertex set are ‘jointly connected’. Bollobás, Riordan, Slivken, and Smith (2017) proved that, when the two graphs are independent binomial random graphs, whether the jigsaw process percolates undergoes a phase transition when the product of the two probabilities is 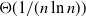$\Theta({1}/{(n\ln n)})$. We show that this threshold is sharp, and that it lies at 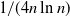${1}/{(4n\ln n)}$.

Keywords

Jigsaw percolationrandom graphphase transitionsharp threshold

MSC classification

Primary: 05C80: Random graphs
Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 60C05: Combinatorial probability
Type
Original Article
Information
Advances in Applied Probability , Volume 51 , Issue 2 , June 2019 , pp. 378 - 407
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, G. E., Askey, R. and Roy, R. (1999). Special Functions (Encyclopedia Math. Appl. 71). Cambridge University Press.Google Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286 , 509–512.CrossRefGoogle ScholarPubMed
Bollobás, B. and Thomason, A. (1985). Random Graphs of Small Order (North-Holland Math. Stud. 118). North-Holland, Amsterdam, pp. 47–97.CrossRefGoogle Scholar
Bollobás, B., Cooley, O., Kang, M. and Koch, C. (2017). Jigsaw percolation on random hypergraphs. J. Appl. Prob. 54 , 1261–1277.CrossRefGoogle Scholar
Bollobás, B., Riordan, O., Slivken, E., and Smith, P. (2017). The threshold for jigsaw percolation on random graphs. Electron. J. Combinatorics 24, 14pp.Google Scholar
Bollobás, B., Riordan, O., Spencer, J. and Tusnády, G. (2001). The degree sequence of a scale-free random graph process. Random Structures Algorithms 18 , 279–290.CrossRefGoogle Scholar
Brummitt, C. D., Chatterjee, S., Dey, P. S., and Sivakoff, D. (2015). Jigsaw percolation: What social networks can collaboratively solve a puzzle? Ann. Appl. Prob. 25 , 2013–2038.CrossRefGoogle Scholar
Buldyrev, S. V., Parshani, R., Paul, G., Stanley, H. E. and Havlin, S. (2010). Catastrophic cascade of failures in interdependent networks. Nature 464 , 1025–1028.CrossRefGoogle ScholarPubMed
Cooley, O. and Gutiérrez, A. (2017). Multi-coloured jigsaw percolation on random graphs. Preprint. Available at https://arxiv.org/abs/1712.00992.Google Scholar
Erdös, P. and Rényi, A. (1959). On random graphs. I. Publ. Math. Debrecen 6 , 290–297.Google Scholar
Gravner, J. and Sivakoff, D. (2017). Nucleation scaling in jigsaw percolation. Ann. Appl. Prob. 27 , 395–438.CrossRefGoogle Scholar
Janson, S., uczak, T., and Ruciski, A. (2000). Random Graphs (Wiley-Interscience Series in Discrete Mathematics and Optimization). Wiley-Interscience, New York.CrossRefGoogle Scholar
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A. and Boguñá, M. (2010). Hyperbolic geometry of complex networks. Phys. Rev. E (3) 82, 18pp.CrossRefGoogle ScholarPubMed
Robbins, H. (1955). A remark on Stirling’s formula. Amer. Math. Monthly 62 , 26–29.Google Scholar