Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T14:56:27.257Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrence criteria for multi-dimensional Markov chains and multi-dimensional linear birth and death processes

Published online by Cambridge University Press:  01 July 2016

Harry Kesten
Harry Kesten*
Affiliation:
Cornell University
Get access Rights & Permissions [Opens in a new window]

Abstract

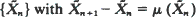Criteria are established for a discrete-time Markov process {Xn}n≧0 in Rd to have strictly positive, respectively zero, probability of escaping to infinity. These criteria are mainly in terms of the mean displacement vectors μ(y) = E{Xn+1|Xn = y} – y, and are essentially such that they force a deterministic process w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.

Keywords

MULTI-DIMENSIONAL MARKOV PROCESSMULTI-DIMENSIONAL BIRTH AND DEATH PROCESSTRANSIENTRECURRENTESCAPE TO INFINITY
Type
Research Article
Information
Advances in Applied Probability , Volume 8 , Issue 1 , March 1976 , pp. 58 - 87
Copyright
Copyright © Applied Probability Trust 1976 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Breiman, L. (1968) Probability. Addison-Wesley, San Francisco.Google Scholar
[2] Chung, K. L. (1967) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, New York.Google Scholar
[3] Freedman, D. (1971) Markov Chains. Holden-Day, San Francisco.Google Scholar
[4] Friedman, A. (1973) Wandering out to infinity of diffusion processes. Trans. Amer. Math. Soc. 184, 185–203.Google Scholar
[5] Iglehart, D. L. (1964) Multivariate competition processes. Ann. Math. Statist. 35, 350–361.CrossRefGoogle Scholar
[6] Karlin, S. and Kaplan, N. (1973) Criteria for extinction of certain population growth processes with interacting types. Adv. Appl. Prob. 5, 183–199.CrossRefGoogle Scholar
[7] Kesten, H. (1970) Quadratic transformations: a model for population growth II. Adv. Appl. Prob. 2, 179–228.CrossRefGoogle Scholar
[8] Kesten, H. (1972) Limit theorems for stochastic growth models. Adv. Appl. Prob. 4, 193–232 and 393–428.CrossRefGoogle Scholar
[9] Kesten, H. and Stigum, B. P. (1975) Balanced growth under uncertainty in decomposable economics. In Essays on Economic Behaviour Under Uncertainty, ed. Balch, M. S., McFadden, D. L. and Wu, S. Y., American Elsevier, New York, 339–381.Google Scholar
[10] Lamperti, J. (1960) Criteria for the recurrence or transience of stochastic processes I. J. Math. Anal. Appl. 1, 314–330.CrossRefGoogle Scholar
[11] Milch, P. R. (1968) A multi-dimensional linear growth birth and death process. Ann. Math. Statist. 39, 727–754.CrossRefGoogle Scholar
[12] Pinsky, M. A. (1974) Stochastic stability and the Dirichlet problem. Comm. Pure Appl. Math. 27, 311–350.CrossRefGoogle Scholar
[13] Reuter, G. E. H. (1961) Competition processes. Proc. 4th Berkeley Symp. Math. Statist. Prob. 2, 421–430.Google Scholar
[14] Tanny, D. (1975) Branching Processes in Random Environments. , Cornell University.Google Scholar
[15] Whittle, P. (1969) Refinements of Kolmogorov's inequality. Teor. Veroyat. Primen. 14, 315–317 (Theor. Prob. Appl. 14, 310–311).Google Scholar