No CrossRef data available.
Published online by Cambridge University Press: 01 July 2016
The shift method consists in computing the expectation of an integrable functional F defined on the probability space ((ℝd)N, B(ℝd)⊗N, μ⊗N) (μ is a probability measure on ℝd) using Birkhoff's Pointwise Ergodic Theorem, i.e.
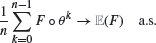
as n → ∞, where θ denotes the canonical shift operator. When F lies in L2(FT, μ⊗N) for some integrable enough stopping time T, several weak (CLT) or strong (Gàl-Koksma Theorem or LIL) converging rates hold. The method successfully competes with Monte Carlo. The aim of this paper is to extend these results to more general probability distributions P on ((ℝd)N, B(ℝd)⊗N), namely when the canonical process (Xn)n∊N is P-stationary, α-mixing and fulfils Ibragimov's assumption
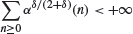
for some δ > 0. One application is the computation of the expectation of functionals of an α-mixing Markov Chain, under its stationary distribution Pν. It may both provide a better accuracy and save the random number generator compared to the usual Monte Carlo or shift methods on independent innovations.