Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T14:11:53.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Random high-dimensional orders

Part of: Ordered sets Combinatorial probability

Published online by Cambridge University Press:  01 July 2016

Béla Bollobás  and
Graham Brightwell
Béla Bollobás*
Affiliation:
University of Cambridge
Graham Brightwell*
Affiliation:
London School of Economics and Political Science
*
* Postal address: Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, 16 Mill Lane, Cambridge, CB2 1SB, UK.
** Postal address: Department of Mathematics, London School of Economics and Political Science, Houghton Street, London, WC2A 2AE, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

The random k-dimensional partial order Pk(n) on n points is defined by taking n points uniformly at random from [0,1]k. Previous work has concentrated on the case where k is constant: we consider the model where k increases with n.

We pay particular attention to the height Hk(n) of Pk(n). We show that k = (t/log t!) log n is a sharp threshold function for the existence of a t-chain in Pk(n): if k – (t/log t!) log n tends to + ∞ then the probability that Pk(n) contains a t-chain tends to 0; whereas if the quantity tends to − ∞ then the probability tends to 1. We describe the behaviour of Hk(n) for the entire range of k(n).

We also consider the maximum degree of Pk(n). We show that, for each fixed d ≧ 2, 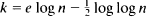is a threshold function for the appearance of an element of degree d. Thus the maximum degree undergoes very rapid growth near this value of k.

We make some remarks on the existence of threshold functions in general, and give some bounds on the dimension of Pk(n) for large k(n).

Keywords

RANDOM PARTIAL ORDERORDER DIMENSION

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 06A06: Partial order, general
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 27 , Issue 1 , March 1995 , pp. 161 - 184
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Arratia, R., Goldstein, L. and Gordon, L. (1989) Two moments suffice for Poisson approximation: the Stein–Chen method. Ann. Prob. 17, 9–25.CrossRefGoogle Scholar
[2] Barbour, A. D. and Eagleson, G. K. (1982) Poisson approximation for some statistics based on exchangeable trials. Adv. Appl. Prob. 15, 585–600.CrossRefGoogle Scholar
[3] Bollobás, B. (1985) Random Graphs. Academic Press, London.Google Scholar
[4] Bollobás, B. (1991) Random Graphs. In Probabilistic Combinatorics and its Applications , Proceedings of Symposia in Applied Mathematics 44, pp. 1–20. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
[5] Bollobás, B. and Brightwell, G. (1992). The height of a random partial order: concentration of measure. Ann. Appl. Prob. 2, 285–301.Google Scholar
[6] Bollobás, B. and Janson, S. (1994). On the length of a longest increasing subsequence in a random permutation. Submitted.Google Scholar
[7] Bollobás, B. and Winkler, P. M. (1988) The longest chain among random points in Euclidean space. Proc. Amer. Math. Soc. 103, 347–353.Google Scholar
[8] Brightwell, G. (1992) Random k-dimensional orders: width and number of linear extensions. Order 9, 333–342.Google Scholar
[9] Brightwell, G. and Trotter, W. T. (1994) Incidence posets of trees in posets of large dimensions. Order. To appear.Google Scholar
[10] Chen, L. H. Y. (1975) Poisson approximation for dependent trials. Ann. Prob. 3, 534–535.CrossRefGoogle Scholar
[11] Frieze, A. M. (1991). On the length of the longest monotone subsequence in a random permutation. Ann. Appl. Prob. 1, 301–305.Google Scholar
[12] Trotter, W. T. (1992) Combinatorics and Partially Ordered Sets: Dimension Theory. Johns Hopkins University Press, Baltimore.Google Scholar
[13] Winkler, P. M. (1985) Random orders. Order 1, 317–335.CrossRefGoogle Scholar
[14] Winkler, P. M. (1985) Connectedness and diameter for random orders of fixed dimension. Order 2, 165–171.CrossRefGoogle Scholar
[15] Winkler, P. M. (1991) Random orders of dimension 2. Order 7, 329–339.Google Scholar