Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T16:23:15.365Z Has data issue: false hasContentIssue false
  • English
  • Français

On the time constant and path length of first-passage percolation

Published online by Cambridge University Press:  01 July 2016

Harry Kesten
Harry Kesten*
Affiliation:
Cornell University
*
∗Postal address: Department of Mathematics, White Hall, Cornell University, Ithaca, NY 14853, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

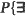Let U be the distribution function of the passage time of an individual bond of the square lattice, and let pT be the critical probability above which the expected size of the open component of the origin (in the usual bond percolation) is infinite. It is shown that if (∗)U(0–) = 0, U(0) < pT, then there exist constants 0 < a, C1 < ∞ such that a self-avoiding path of at least n steps starting at the origin and with passage time ≦ an} ≦ 2 exp (–C1n).

From this it follows that under (∗) the time constant μ (U) of first-passage percolation is strictly positive and that for each c > 0 lim sup (1/n)Nn(c) <∞, where Nn(c) is the maximal number of steps in the paths starting at the origin with passage time at most cn.

Keywords

FIRST-PASSAGE PERCOLATIONBERNOULLI PERCOLATIONTIME CONSTANTROUTE LENGTH
Type
Research Article
Information
Advances in Applied Probability , Volume 12 , Issue 4 , December 1980 , pp. 848 - 863
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Cox, J. T. and Durrett, T. (1980). Some limit theorems for percolation processes with necessary and sufficient conditions. Ann. Prob. To appear.Google Scholar
[2] Hammersley, J. M. and Welsh, D. J. A. (1965) First-passage percolation, subadditive processes, stochastic networks, and generalized renewal theory. In Bernoulli, Bayes, Laplace Anniversary Volume , ed. Neyman, J. and LeCam, L. M., Springer-Verlag, Berlin.Google Scholar
[3] Russo, L. (1978) A note on percolation. Z. Wahrscheinlichkeitsth. 43, 39–48.Google Scholar
[4] Seymour, P. D. and Welsh, D. J. A. (1978) Percolation probabilities on the square lattice. Ann. Discrete Math. 3, 227–245.Google Scholar
[5] Smythe, R. T. and Wierman, J. C. (1978) First passage percolation on the square lattice. Lecture Notes in Mathematics 671, Springer-Verlag, Berlin.Google Scholar
[6] Wierman, J. C. (1980) Weak moment conditions for time coordinates in first-passage percolation models. J. Appl. Prob. 17,Google Scholar
[7] Wierman, J. C. and Reh, E. (1978) On conjectures in first-passage percolation theory. Ann. Prob. 6, 388–397.CrossRefGoogle Scholar