Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-09T07:29:00.114Z Has data issue: false hasContentIssue false
  • English
  • Français

On the settling time of the congested GI/G/1 queue

Published online by Cambridge University Press:  01 July 2016

George D. Stamoulis  and
John N. Tsitsiklis
George D. Stamoulis*
Affiliation:
Massachusetts Institute of Technology
John N. Tsitsiklis*
Affiliation:
Massachusetts Institute of Technology
*
∗Postal address for both authors: Laboratory for Information and Decision Systems, Massachusetts Institute of Technology, Cambridge, MA 02139, USA.
∗Postal address for both authors: Laboratory for Information and Decision Systems, Massachusetts Institute of Technology, Cambridge, MA 02139, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze a stable GI/G/1 queue that starts operating at time t = 0 with N0 ≠ 0 customers. First, we analyze the time 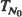required for this queue to empty for the first time. Under the assumption that both the interarrival and the service time distributions are of the exponential type, we prove that 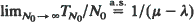, where λ and μ are the arrival and the service rates. Furthermore, assuming in addition that the interarrival time distribution is of the non-lattice type, we show that the settling time of the queue is essentially equal to N0/(μ –λ); that is, we prove that 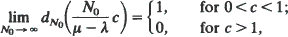where 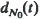is the total variation distance between the distribution of the number of customers in the system at time t and its steady-state distribution. Finally, we show that there is a similarity between the queue we analyze and a simple fluid model.

Keywords

CONGESTED QUEUESETTLING TIMETRANSIENT ANALYSIS
Type
Research Article
Information
Advances in Applied Probability , Volume 22 , Issue 4 , December 1990 , pp. 929 - 956
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by the NSF under Grant ECS-8552419, with matching funds from Bellcore Inc. and Du Pont, and the ARO under Grant DAAL03-86-K-0171.

References

1. Aldous, D. (1983) Random walks on finite groups and rapidly mixing Markov chains. Séminaire de Probabilités XVII, Lecture Notes in Mathematics 986, Springer-Verlag, Berlin, 243–297.Google Scholar
2. Anantharam, V. (1988) The settling time of a closed network. Unpublished.Google Scholar
3. Bahadur, R. R. (1971) Some Limit Theorems in Statistics. SIAM, Philadelphia.Google Scholar
4. Bateman Manuscript Project (1954) Tables of Integral Transforms , Vol. 1. McGraw-Hill, New York.Google Scholar
5. Borovkov, A. A. (1976) Stochastic Processes in Queueing Theory. Springer-Verlag, Berlin.Google Scholar
6. Cohen, J. W. (1969) The Single-Server Queue. North-Holland, Amsterdam.Google Scholar
7. Ellis, R. S. (1985) Entropy, Large Deviations, and Statistical Mechanics . Springer-Verlag, Berlin.Google Scholar
8. Hajek, B. (1982) Hitting-time and occupation-time bounds implied by drift analysis with applications. Adv. Appl. Prob. 14, 502–525.Google Scholar
9. Heyman, D. P. and Sobel, M. J. (1982) Stochastic Methods in Operations Research , Vol. 1. McGraw-Hill, New York.Google Scholar
10. Kleinrock, L. (1975) Queueing Systems, Vol. 1: Theory. Wiley, New York.Google Scholar
11. Pollaczek, F. (1952) Sur la répartition des périodes d'occupation ininterrompue d'un guichet. C.R. Acad. Sci. Paris 234, 2042–2044.Google Scholar
12. Prabu, N. U. (1980) Stochastic Storage Processes. Springer-Verlag, Berlin.Google Scholar
13. Stamoulis, G. D. (1988) Transient Analysis of Some Open Queueing Systems. S.M. Thesis. Technical Report LIDS-TH-1976, MIT.Google Scholar
14. Takács, L. (1962) Introduction to the Theory of Queues. Oxford University Press, New York.Google Scholar