Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T02:04:05.671Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic distributions of maxima of trigonometric polynomials with random coefficients

Published online by Cambridge University Press:  01 July 2016

K. F. Turkman  and
A. M. Walker
K. F. Turkman*
Affiliation:
University of Sheffield
A. M. Walker*
Affiliation:
University of Sheffield
*
∗Present address: Faculdade de Ciencias de Universidade de Lisboa, Departamento da Estatistica, Investigaçao Operacional e Computacao, 58 Rua da Escola Politecnica, 1294 Lisboa Codex, Portugal.
∗∗ Postal address: Department of Probability and Statistics, The University, Sheffield S3 7RH, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

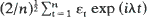Let {ε t, t = 1, 2, ···, n} be a sequence of mutually independent standard normal random variables. Let Xn(λ) and Yn(λ) be respectively the real and imaginary parts of exp iλ t, and let 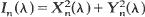. It is shown that as n tends to∞, the distribution functions of the normalized maxima of the processes {Xn(λ)}, (Yn(λ)}, {In(λ)} over the interval λ∈ [0,π] each converge to the extremal distribution function exp [–e–x], —∞ < x <∞.

It is also shown that these results can be extended to the case where {ε t} is a stationary Gaussian sequence with a moving-average representation.

Keywords

PERIODOGRAMEXTREME-VALUE DISTRIBUTIONS
Type
Research Article
Information
Advances in Applied Probability , Volume 16 , Issue 4 , December 1984 , pp. 819 - 842
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berman, S. M. (1983) Sojourns and extremes of Fourier sums and series with random coefficients. Stoch. Proc. Appl. 15, 213–238.Google Scholar
Hannan, E. J. (1961) Testing for a jump in the spectral function. J. R. Statist. Soc. B 23, 394–404.Google Scholar
Leadbetter, M. R. (1967) A note on the moments of the number of axis crossings by a stochastic process. Bull. Amer. Math. Soc. 73, 129–132.Google Scholar
Leadbetter, M. R. (1978) On extremes of stationary processes. Mimeo Series No. 1194, Institute of Statistics, University of North Carolina at Chapel Hill.Google Scholar
Marcus, M. B. (1977) Level crossings of a stochastic process with absolutely continuous sample paths. Ann. Prob. 5, 52–71.CrossRefGoogle Scholar
Turkman, K. F. (1980) Limiting Distributions of Maxima of Certain Types of Non-Stationary Stochastic Processes. , University of Sheffield.Google Scholar
Walker, A. M. (1965) Some asymptotic results for the periodogram of a stationary time series. J. Austral. Math. Soc. 5, 107–128.Google Scholar
Whittle, P. (1959) Sur la distribution du maximum d'un polynome trigonometrique à coefficients aléatoires. Colloq. Internat. CNRS 87, 173–184.Google Scholar
Zygmund, A. (1959) Trigonometric Series, Vol. 2. Cambridge University Press.Google Scholar