Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T13:39:13.624Z Has data issue: false hasContentIssue false
  • English
  • Français

On a mixed singular/switching control problem with multiple regimes

Part of: Stochastic systems and control Hamilton-Jacobi theories, including dynamic programming Control systems

Published online by Cambridge University Press:  22 August 2022

Mark Kelbert  and
Harold A. Moreno-Franco Open the ORCID record for Harold A. Moreno-Franco [Opens in a new window]
Mark Kelbert*
Affiliation:
HSE University
Harold A. Moreno-Franco*
Affiliation:
HSE University
*
*Postal address: National Research University Higher School of Economics (HSE), Faculty of Economics, Department of Statistics and Data Analysis, Moscow, Russian Federation.
*Postal address: National Research University Higher School of Economics (HSE), Faculty of Economics, Department of Statistics and Data Analysis, Moscow, Russian Federation.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies a mixed singular/switching stochastic control problem for a multidimensional diffusion with multiple regimes on a bounded domain. Using probabilistic partial differential equation and penalization techniques, we show that the value function associated with this problem agrees with the solution to a Hamilton–Jacobi–Bellman equation. In this way, we see that the regularity of the value function is 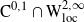$ \textrm{C}^{0,1}\cap \textrm{W}^{2,\infty}_{\textrm{loc}}$ .

Keywords

Singular/switching stochastic control problemHamilton–Jacobi–Bellman equationsnonlinear partial differential system

MSC classification

Primary: 49L99: None of the above, but in this section
Secondary: 93E20: Optimal stochastic control 93C30: Systems governed by functional relations other than differential equations (such as hybrid and switching systems)
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 3 , September 2022 , pp. 743 - 782
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, R. and Fournier, J. (2003). Sobolev Spaces, 2nd edn. Elsevier, Amsterdam.Google Scholar
Azcue, P. and Muler, N. (2015). Optimal dividend payment and regime switching in a compound Poisson risk model. SIAM J. Control Optimization 53, 3270–3298.CrossRefGoogle Scholar
Chevalier, E., Gaïgi, M. and Ly Vath, V. (2017). Liquidity risk and optimal dividend/investment strategies. Math. Financial Econom. 11, 111–135.CrossRefGoogle Scholar
Chevalier, E., Ly Vath, V. and Scotti, S. (2013). An optimal dividend and investment control problem under debt constraints. SIAM J. Financial Math. 4, 297–326.CrossRefGoogle Scholar
Csató, G., Dacorogna, B. and Kneuss, O. (2012). The Pullback Equation for Differential Forms. Birkhäuser, Boston.CrossRefGoogle Scholar
Davis, M. and Zervos, M. (1998). A pair of explicitly solvable singular stochastic control problems. Appl. Math. Optimization 38, 327–352.CrossRefGoogle Scholar
Evans, L. (1979). A second-order elliptic equation with gradient constraint. Commun. Partial Differential Equat. 4, 555–572.CrossRefGoogle Scholar
Evans, L. (2010). Partial Differential Equations, 2nd edn. American Mathematical Society, Providence, RI.Google Scholar
Garroni, M. and Menaldi, J. (2002). Second Order Elliptic Integro-differential Problems. Chapman & Hall/CRC, New York.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. (2001). Elliptic Partial Differential Equations of Second Order. Springer, Berlin.CrossRefGoogle Scholar
Guo, X. and Tomecek, P., (2008). Connections between singular control and optimal switching. SIAM J. Control Optimization 47, 421–443.CrossRefGoogle Scholar
Kelbert, M. and Moreno-Franco, H. A. (2019). HJB equations with gradient constraint associated with controlled jump-diffusion processes. SIAM J. Control Optimization 57, 2185–2213.CrossRefGoogle Scholar
Lenhart, S. and Belbas, S. (1983). A system of nonlinear partial differential equations arising in the optimal control of stochastic systems with switching costs. SIAM J. Appl. Math. 43, 465–475.CrossRefGoogle Scholar
Lions, P. (1983). A remark on Bony maximum principle. Proc. Amer. Math. Soc. 88, 503–508.CrossRefGoogle Scholar
Ly Vath, V., Pham, H., and Villeneuve, S. (2008). A mixed singular/switching control problem for a dividend policy with reversible technology investment. Ann. Appl. Prob. 18, 1164–1200.CrossRefGoogle Scholar
Pham, H. (2009). Continuous-Time Stochastic Control and Optimization with Financial Applications. Springer, Berlin.CrossRefGoogle Scholar
Protter, P. (2005). Stochastic Integration and Differential Equations, 2nd edn. Springer, Berlin.CrossRefGoogle Scholar
Yamada, N. (1988). The Hamilton–Jacobi–Bellman equation with a gradient constraint. J. Differential Equat. 71, 185–199.CrossRefGoogle Scholar
Zhu, H. (1992). Generalized solution in singular stochastic control: the nondegenerate problem. Appl. Math. Optimization 25, 225–245.CrossRefGoogle Scholar