Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T16:23:34.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Networks and dynamical systems

Part of: Special processes Markov processes

Published online by Cambridge University Press:  01 July 2016

V. A. Malyshev
V. A. Malyshev*
Affiliation:
INRIA
*
∗Postal address: INRIA—Domaine de Voluceau, Rocquencourt, BP105, 78153 Le Chesnay, France. On leave from Laboratory of Large Random Systems, Moscow State University, Moscow, 119899, Russia.
Get access Rights & Permissions [Opens in a new window]

Abstract

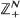A new approach to the problem of classification of (deflected) random walks in or Markovian models for queueing networks with identical customers is introduced. It is based on the analysis of the intrinsic dynamical system associated with the random walk. Earlier results for small dimensions are presented from this novel point of view. We give proofs of new results for higher dimensions related to the existence of a continuous invariant measure for the underlying dynamical system. Two constants are shown to be important: the free energy M < 0 corresponds to ergodicity, the Lyapounov exponent L < 0 defines recurrence. General conjectures, examples, unsolved problems and surprising connections with ergodic theory, classical dynamical systems and their random perturbations are largely presented. A useful notion naturally arises, the so-called scaled random perturbation of a dynamical system.

Keywords

CLASSIFICATION OF MARKOV PROCESSESSINGLE-CUSTOMER QUEUEING NETWORKSSCALING LIMIT FOR DEFLECTED RANDOM WALKSRANDOM WALKS IN AN ORTHANT

MSC classification

Primary: 60J99: None of the above, but in this section
Secondary: 60K25: Queueing theory 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 1 , March 1993 , pp. 140 - 175
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

References

[1] Arnold, L., Oeljeklaus, E. and Pardoux, E. (1986) Almost sure and moment stability for linear Ito equations. In Lyapounov Exponents, Lecture Notes in Mathematics 1186, pp. 129–159, Springer-Verlag, Berlin.Google Scholar
[2] Arnold, V. I. (1983) Geometrical Methods in the Theory of Ordinary Differential Equations. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[3] Baccelli, F. and Makowski, A. M. (1989) Queueing models for systems with synchronization constraints, Proc. IEEE 77, 138–161.CrossRefGoogle Scholar
[4] Blank, M. L. (1989) Small perturbations of chaotic dynamical systems. Uspehi Mat. Nauk. 44(6), 3–28.Google Scholar
[5] Borovkov, A. A. (1990) Lyapounov functions and ergodicity of multidimensional Markov chains. Institute of Mathematics of Siberian Ac. of Sci. Preprint No. 19, Novosibirsk.Google Scholar
[6] Botvich, D. D. and Zamyatin, A. (1991) Lyapounov functions for some BCMP and Kelly networks with conservative disciplines. Preprint, Moscow State University.Google Scholar
[7] Bougerol, P. (1986) Oscillation de produits de matrices aléatoires dont l'exposant de Lyapunov est nul. In Lyapunov Exponents, Lecture Notes in Mathematics 1186, 27–36.CrossRefGoogle Scholar
[8] Chung, K. L. (1967) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, Berlin.Google Scholar
[9] Doob, J. L. (1959) Discrete potential theory and boundaries. J. Math. Mech. 8, 433–458.Google Scholar
[10] Fayolle, G. and Iasnogorodski, R. (1979) Two coupled processors: the reduction to a Riemann–Hilbert problem. Z. Wahrschlichkeitsth. 47, 325–351.CrossRefGoogle Scholar
[11] Fayolle, G., Ignatyuk, I. A., Malyshev, V. A. and Menshikov, M. V. (1991) Random walks in two dimensional complexes. QUESTA 9, 269–300.Google Scholar
[12] Fayolle, G., Malyshev, V. A. and Menshikov, M. V. (1992) Random walks in a quarter plane with zero drift. 1: ergodicity and null recurrence. Ann. Inst. H. Poincaré 28, 179–194.Google Scholar
[13] Fayolle, G., Malyshev, V. A., Menshikov, M. V. and Sidorenko, A. F. (1991) Lyapounov functions for Jackson networks. Rapport de Recherche INRIA, no. 1380.Google Scholar
[14] Feller, W. (1956) Boundaries induced by positive matrices. Trans. Amer. Math. Soc. 83, 19–54.CrossRefGoogle Scholar
[15] Filonov, Yu. P. (1989) Ergodicity criteria for homogeneous discrete Markov chains. Ukrainian Math. J. 41, 1421–1422.CrossRefGoogle Scholar
[16] Fomin, S. V., Kornfeld, I. P. and Sinai, Ya. G. (1980) Ergodic Theory. Nauka, Moscow.Google Scholar
[17] Foster, F. G. (1953) On stochastic matrices associated with certain queueing processes. Ann. Math. Statist. 24, 355–360.CrossRefGoogle Scholar
[18] Freidlin, M. I. and Wentzell, A. D. (1984) Random Perturbations of Dynamical Systems. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[19] Genis, I. L. and Krylov, N. V. (1973) About exact barriers in the problem with oblique derivative. Siberian Math. J. 14, 36–43.CrossRefGoogle Scholar
[20] Has'Minski, R. Z. (1967) Necessary and sufficient conditions for the asymptotic stability of linear stochastic systems. Theory Prob. Appl. 12, 144–147.Google Scholar
[21] Has'Minski, R. Z. (1980) Stochastic Stability of Differential Equations. Sijthoff and Noordhoof, Alphenan den Rijn.CrossRefGoogle Scholar
[22] Ignatyuk, I. A. and Malyshev, V. A. (1991) Classification of random walks in ℤ4 + . Selecta Math. Sov. To appear.Google Scholar
[23] Katok, A. and Kifer, Yu. (1986) Random perturbations of transformations of an interval. J. Anal. Math. 47, 193–237.CrossRefGoogle Scholar
[24] Kelbert, M. and Suhov, Yu. (1988) Mathematical problems of queueing networks. In Probability theory. Mathematical Statistics. Theoretical cybernetics. Itogi nauki i tecniki, Akad. Nauk SSSR, Vsesoyuz. Inst. Naucn. i Techn. Informacii, Moscow , 26, 3–96.Google Scholar
[25] Kelly, F. P. (1991) Loss networks. Ann. Appl. Prob. 1, 319–378.CrossRefGoogle Scholar
[26] Kifer, Yu. (1986) Ergodic Theory of Random Transformations. Birkhäuser, Basel.CrossRefGoogle Scholar
[27] Kifer, Yu. (1986) General random perturbations of hyperbolic and expanding transformations. J. Anal. Math. 47, 11–150.CrossRefGoogle Scholar
[28] Kifer, Yu. (1990) Principal eigenvalues, topological pressure and stochastic stability of equilibrium states. Israel J. Math. 70, 1–47.CrossRefGoogle Scholar
[29] Malyshev, V. A. (1970) Random Walks. The Wiener–Hopf Equations in a Quadrant of the Plane. Galois Automorphisms. Moscow State University Press.Google Scholar
[30] Malyshev, V. A. (1972) Classification of two-dimensional random walks and almost linear semimartingales. Dokl. Akad. Nauk USSR 202, 526–528.Google Scholar
[31] Malyshev, V. A. and Menshikov, M. V. (1979) Ergodicity, continuity and analyticity of countable Markov chains. Trans. Moscow. Math. Soc. 39, 3–48.Google Scholar
[32] Malyshev, V. A. and Minlos, R. A. (1985) Gibbs Random Fields. Method of Cluster Expansions. Kluwer, Dordrecht.Google Scholar
[33] Mane, R. (1987) Ergodic Theory and Differentiable Dynamics. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[34] Menshikov, M. V. (1974) Ergodicity and transience conditions for random walks in the positive octant of space. Dokl. Akad. Nauk SSSR 217, 755–758.Google Scholar
[35] Mertens, J.-F., Samuel-Kahn, E. and Zamir, S. (1978) Necessary and sufficient conditions for recurrence and transience of Markov chains in terms of inequalities. J. Appl. Prob. 15, 848–851.CrossRefGoogle Scholar
[36] Mikhailov, V. A. (1988) Geometric analysis of stability of Markov chains in ℤ N + and its applications. Prob. Informat. Trans. 24, 61–67.Google Scholar
[37] Oseledec, V. I. (1968) Multiplicative ergodic theorem. Characteristic Lyapounov exponents of dynamical systems. Trudy Moscow Math. Soc. 19, 179–210.Google Scholar
[38] Reiman, M. I. and Williams, R. J. (1988) A boundary property of semimartingale reflecting brownian motions. Prob. Theory Rel. Fields 77, 87–97.CrossRefGoogle Scholar
[39] Ruelle, D. (1978) Thermodynamic Formalism. Addison-Wesley, Reading, MA.Google Scholar
[40] Rybko, A. N. and Stolyar, A. L. (1992) On the problem of ergodicity of Markov processes corresponding to the message switching networks. Probl. Informat. Trans. 28, 3–26.Google Scholar
[41] Sinai, Ya. G. (1972) Gibbs measures in ergodic theory. Uspekhi Mat. Nauk. 27(4), 21–64.Google Scholar
[42] Szpankowski, W. (1990) Towards computable stability criteria for some multidimensional stochastic processes. In Stochastic Analysis of Computer and Communication Systems ed. Takagi, H. North-Holland, Amsterdam.Google Scholar
[43] Tweedie, R. L. (1976) Criteria for classifying general Markov chains. Adv. Appl. Prob. 8, 737–771.CrossRefGoogle Scholar
[44] Varadhan, S. R. S. and Williams, R. J. (1985) Brownian motion in a wedge with oblique reflection. Commun. Pure Appl. Math. 38, 405–443.CrossRefGoogle Scholar
[45] Walters, P. (1975) An Introduction to Ergodic Theory. Springer-Verlag, Berlin.Google Scholar
[46] Williams, R. J. (1985) Recurrence classification and invariant measure for reflected brownian motion in a wedge. Ann. Prob. 13, 758–778.CrossRefGoogle Scholar
[47] Willms, J. (1988) Asymptotic behaviour of iterated piecewise monotone maps. Erg. Theory Dyn. Syst. 8, 111–131.CrossRefGoogle Scholar
[48] Young, L. S. (1986) Stochastic stability of hyperbolic attractors. Erg. Theory Dyn. Syst. 6, 311–319.CrossRefGoogle Scholar

References added in proof

[49] Botvich, D. D. and Zamyatin, A. (1992) Ergodic properties of queueing networks with batch arrivals and batch service. Rapport de recherche, INRIA.Google Scholar
[50] Chen, H. and Mabdekbaynm, A. (1991) Discrete flow networks: bottleneck analysis and fluid approximations. Math. Operat. Res. 16, 408–446.CrossRefGoogle Scholar
[51] Malyshev, V. A. (1992) Stabilization laws for processes with a localized interaction. Rapport de recherche, INRIA.Google Scholar