Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T13:42:56.998Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Probability Metrics and Their Generating Classes of Functions

Part of: Distribution theory - Probability Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  01 July 2016

Alfred Müller
Alfred Müller*
Affiliation:
Universität Karlsruhe
*
∗ Postal address: Institut für Wirtschaftstheorie und Operations Research, Universität Karlsruhe, Kaiserstr. 12, D-76128 Karlsruhe, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider probability metrics of the following type: for a class of functions and probability measures P, Q we define 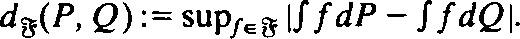A unified study of such integral probability metrics is given. We characterize the maximal class of functions that generates such a metric. Further, we show how some interesting properties of these probability metrics arise directly from conditions on the generating class of functions. The results are illustrated by several examples, including the Kolmogorov metric, the Dudley metric and the stop-loss metric.

Keywords

INTEGRAL PROBABILITY METRICSMAXIMAL GENERATORUNIFORMITY IN WEAK CONVERGENCE: STOP-LOSS METRIC

MSC classification

Primary: 60E05: Distributions
Secondary: 60B10: Convergence of probability measures
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 2 , June 1997 , pp. 429 - 443
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhattacharya, R. N. and Ranga Rao, R. (1976) Normal Approximation and Asymptotic Expansions. Wiley, New York.Google Scholar
Choquet, G. (1969) Lectures on Analysis II. Benjamin, New York.Google Scholar
Dudley, R. M. (1989) Real Analysis and Probability. Wadsworth and Brooks, Belmont, CA.Google Scholar
Gerber, H. U. (1981) An Introduction to Mathematical Risk Theory. Huebner Foundation Monograph.Google Scholar
Hewitt, E. and Stromberg, K. (1965) Real and Abstract Analysis. Springer, Berlin.Google Scholar
Rachev, S. T. (1991) Probability Metrics and the Stability of Stochastic Models. Wiley, New York.Google Scholar
Rachev, S. T. and Rüschendorf, L. (1990) Approximation of sums by compound Poisson distributions with respect to stop-loss distances. Adv. Appl. Prob. 22, 350–374.Google Scholar
Roberts, A. W. and Varberg, D. E. (1973) Convex Functions. Academic Press, New York.Google Scholar
Robertson, A. P. and Robertson, W. (1966) Topological Vector Spaces. Cambridge University Press, Cambridge.Google Scholar
Zolotarev, V. M. (1983) Probability metrics. Theory Prob. Appl. 28, 278–302.Google Scholar