Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T06:03:28.782Z Has data issue: false hasContentIssue false
  • English
  • Français

Integer-valued branching processes with immigration

Published online by Cambridge University Press:  01 July 2016

F. W. Steutel ,
W. Vervaat  and
S. J. Wolfe
F. W. Steutel*
Affiliation:
University of Technology, Eindhoven
W. Vervaat*
Affiliation:
Catholic University, Nijmegen
S. J. Wolfe*
Affiliation:
University of Delaware
*
∗Postal address: Department of Mathematics, University of Technology, 5600 MB Eindhoven, The Netherlands.
∗∗Postal address: Mathematisch Instituut, Katholieke Universiteit, Toernooiveld, 6525 ED Nijmegen. The Netherlands.
∗∗∗Postal address: Sharp Laboratory, University of Delaware, Newark, DE 19711, U.S.A. Supported by NSF grants MCS 78-02566 and MCS 80-26546.
Get access Rights & Permissions [Opens in a new window]

Abstract

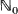The notion of self-decomposability for -valued random variables as introduced by Steutel and van Harn [10] and its generalization by van Harn, Steutel and Vervaat [5], are used to study the limiting behaviour of continuous-time Markov branching processes with immigration. This behaviour provides analogues to the behaviour of sequences of random variables obeying a certain difference equation as studied by Vervaat [12] and their continuous-time counterpart considered by Wolfe [13]. An application in queueing theory is indicated. Furthermore, discrete-state analogues are given for results on stability in the processes studied by Wolfe, and for results on self-decomposability in supercritical branching processes by Yamazato [14].

Keywords

STOCHASTIC DIFFERENCE EQUATIONSTOCHASTIC DIFFERENTIAL EQUATIONSELF-DECOMPOSABLE (CLASS L)STABLE
Type
Research Article
Information
Advances in Applied Probability , Volume 15 , Issue 4 , December 1983 , pp. 713 - 725
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, Berlin.CrossRefGoogle Scholar
[2] Biggins, J. D. and Shanbhag, D. N. (1981) Some divisibility problems in branching processes. Math. Proc. Camb. Phil. Soc. 90, 321–330.CrossRefGoogle Scholar
[3] Foster, J. H. and Williamson, J. S. (1971) Limit theorems for the Galton-Watson process with time-dependent immigration. Z. Wahrscheinlichkeitsth. 20, 227–235.Google Scholar
[4] De Haan, L. (1970) On regular variation and its application to the weak convergence of sample extremes. Mathematical Centre Tracts 32, Mathematical Centre, Amsterdam.Google Scholar
[5] Van Harn, K., Steutel, F. W. and Vervaat, W. (1982) Self-decomposable discrete distributions and branching processes. Z. Wahrscheinlichkeitsth. 61, 97–118.Google Scholar
[6] Harris, T. E. (1963) The Theory of Branching Processes. Springer-Verlag, Berlin.Google Scholar
[7] Jagers, P. and Nerman, O. (1983) Limit theorems for sums determined by branching and other exponentially growing processes. Stoch. Proc. Appl. Google Scholar
[8] Jurek, Z. J. and Vervaat, W. (1983) An integral representation for self-decomposable Banach space valued random variables. Z. Wahrscheinlichkeitsth. 62, 247–262.CrossRefGoogle Scholar
[9] Lukacs, E. (1969) A characterization of stable processes. J. Appl. Prob. 6, 409–418.Google Scholar
[10] Steutel, F. W. and Van Harn, K. (1979) Discrete analogues of self-decomposability and stability. Ann. Prob. 7, 893–899.Google Scholar
[11] Urbanik, K. (1976) Some examples of decomposition semigroups. Bull. Acad. Polon. Sci. Math. 24, 915–918.Google Scholar
[12] Vervaat, W. (1979) On a stochastic difference equation and a representation of non-negative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.Google Scholar
[13] Wolfe, S. J. (1982) On a continuous analogue of the stochastic difference equation Xn= ρXn-1 + Bn . Stoch. Proc. Appl. 12, 301–312.Google Scholar
[14] Yamazato, M. (1975) Some results on infinitely divisible distributions of class L with applications to branching processes. Sci. Rep. Tokyo Kogyo Daigaku, A13, 133–139.Google Scholar