Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T15:38:26.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Fragmentations with self-similar branching speeds

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  22 November 2021

Jean-Jil Duchamps Open the ORCID record for Jean-Jil Duchamps [Opens in a new window]
Jean-Jil Duchamps*
Affiliation:
Université Bourgogne Franche-Comté
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider fragmentation processes with values in the space of marked partitions of 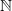$\mathbb{N}$, i.e. partitions where each block is decorated with a nonnegative real number. Assuming that the marks on distinct blocks evolve as independent positive self-similar Markov processes and determine the speed at which their blocks fragment, we get a natural generalization of the self-similar fragmentations of Bertoin (Ann. Inst. H. Poincaré Prob. Statist.38, 2002). Our main result is the characterization of these generalized fragmentation processes: a Lévy–Khinchin representation is obtained, using techniques from positive self-similar Markov processes and from classical fragmentation processes. We then give sufficient conditions for their absorption in finite time to a frozen state, and for the genealogical tree of the process to have finite total length.

Keywords

Self-similarbranching processexchangeablefragmentationrandom partitionrandom treeLévy process

MSC classification

Primary: 60G18: Self-similar processes 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60G09: Exchangeability 60G51: Processes with independent increments; L'evy processes 60G25: Prediction theory
Type
Original Article
Information
Advances in Applied Probability , Volume 53 , Issue 4 , December 2021 , pp. 1149 - 1189
Check for updates
Copyright
© The Author(s) 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Postal address: Laboratoire de mathématiques de Besançon, UMR 6623, CNRS, Université Bourgogne Franche-Comté, 16 route de Gray, 25030 Besançon CEDEX, France.

References

Aldous, D. and Pitman, J. (1998). The standard additive coalescent. Ann. Prob. 26, 1703–1726.CrossRefGoogle Scholar
Berestycki, J. (2002). Ranked fragmentations. ESAIM Prob. Statist. 6, 157–175.CrossRefGoogle Scholar
Bertoin, J. (2002). Self-similar fragmentations. Ann. Inst. H. Poincaré Prob. Statist. 38, 319–340.CrossRefGoogle Scholar
Bertoin, J. (2003). The asymptotic behavior of fragmentation processes. J. Europ. Math. Soc. 5, 395–416.CrossRefGoogle Scholar
Bertoin, J. (2006). Random Fragmentation and Coagulation Processes. Cambridge University Press.CrossRefGoogle Scholar
Bertoin, J. (2008). Homogenenous multitype fragmentations. In In and Out of Equilibrium 2, eds Sidoravicius, V. and Vares, M. E., Birkhäuser, Basel, pp. 161–183.CrossRefGoogle Scholar
Bertoin, J. (2017). Markovian growth-fragmentation processes. Bernoulli 23, 1082–1101.CrossRefGoogle Scholar
Bertoin, J. and Mallein, B. (2019). Infinitely ramified point measures and branching Lévy processes. To appear in Ann. Prob.CrossRefGoogle Scholar
Blancas, A., Duchamps, J.-J., Lambert, A. and Siri-Jégousse, A. (2018). Trees within trees: simple nested coalescents. Electron. J. Prob. 23, 27 pp.CrossRefGoogle Scholar
Chauvin, B. (1991). Product martingales and stopping lines for branching Brownian motion. Ann. Prob. 19, 1195–1205.CrossRefGoogle Scholar
Dadoun, B. (2017). Asymptotics of self-similar growth-fragmentation processes. Electron. J. Prob. 22, 30 pp.CrossRefGoogle Scholar
Daley, D. J. and Vere-Jones, D. (2008). An Introduction to the Theory of Point Processes. Springer, New York.CrossRefGoogle Scholar
Duchamps, J.-J. (2019). Trees within trees II: nested fragmentations. To appear in Ann. Inst. H. Poincaré Prob. Statist.Google Scholar
Ged, F. G. (2019). Profile of a self-similar growth-fragmentation. Electron. J. Prob. 24, 21 pp.CrossRefGoogle Scholar
Haas, B. and Miermont, G. (2004). The genealogy of self-similar fragmentations with negative index as a continuum random tree. Electron. J. Prob. 9, 57–97.CrossRefGoogle Scholar
Haas, B., Miermont, G., Pitman, J. and Winkel, M. (2008). Continuum tree asymptotics of discrete fragmentations and applications to phylogenetic models. Ann. Prob. 36, 1790–1837.CrossRefGoogle Scholar
Haas, B. and Stephenson, R. Scaling limits of multi-type Markov branching trees. In preparation.Google Scholar
Kingman, J. (1982). The coalescent. Stoch. Process. Appl. 13, 235–248.CrossRefGoogle Scholar
Krell, N. (2009). Self-similar branching Markov chains. In Séminaire de Probabilités XLII, eds Donati-Martin, C., émery, M., Rouault, A. and Stricker, C., Springer, Berlin, Heidelberg pp. 261–280.CrossRefGoogle Scholar
Lamperti, J. (1972). Semi-stable Markov processes. I. Z. Wahrscheinlichkeitsth. 22, 205–225.CrossRefGoogle Scholar
Pardo, J. C. and Rivero, V. (2013). Self-similar Markov processes. Bol. Soc. Mat. Mex. 19, 201–235.Google Scholar
Sato, K. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar
Shi, Q. (2017). Growth-fragmentation processes and bifurcators. Electron. J. Prob. 22, 25 pp.CrossRefGoogle Scholar
Srivastava, S. M. (1998). A Course on Borel Sets. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Stephenson, R. (2018). On the exponential functional of Markov additive processes, and applications to multi-type self-similar fragmentation processes and trees. ALEA Latin Amer. J. Prob. Math. Statist. 15, 1257–1292.CrossRefGoogle Scholar