Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T05:21:22.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact distributions for shapes of random triangles in convex sets

Published online by Cambridge University Press:  01 July 2016

D. G. Kendall
D. G. Kendall*
Affiliation:
University of Cambridge
*
∗Postal address: Statistical Laboratory, 16 Mill Lane, Cambridge CB2 1SB, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

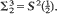The paper starts with a simple direct proof that . A new formula is given for the shape-density for a triangle whose vertices are i.i.d.-uniform in a compact convex set K, and an exact evaluation of that shape-density is obtained when K is a circular disk. An (x, y)-diagram for an auxiliary shape-density 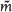is then introduced. When K = circular disk, it is shown that 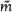is virtually constant over a substantial region adjacent to the relevant section of the collinearity locus, large enough to contain the work-space for most collinearity studies, and particularly appropriate when the ‘strip’ method is used to assess near-collinearity.

Keywords

SHAPE-SPACEAUXILIARY SHAPE-DENSITY(C, W)-DIAGRAM(X, y)-DIAGRAMCOLLINEARITYQUASARS
Type
Research Article
Information
Advances in Applied Probability , Volume 17 , Issue 2 , June 1985 , pp. 308 - 329
Copyright
Copyright © Applied Probability Trust 1985 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ambartzumian, R. V. (1982) Random shapes by factorization. In Statistics in Theory and Practice , ed. Ranneby, B., Umeå.Google Scholar
2. Broadbent, S. R. (1980) Simulating the ley-hunter. J. R. Statist. Soc. A 143, 109–140.Google Scholar
3. Clube, S. V. M. and Trew, A. S. (1983) Observational results on quasar alignments in five fields. In Quasars and Gravitational Lenses (24th Liège Astrophys. Colloq.), 374–377. (See also a further paper by Trew, Clube, and A. Savage submitted to Astron. and Astrophys.).Google Scholar
4. Edmunds, M. G., and George, G. H. (1981) Random alignment of quasars. Nature 290, 481–483.CrossRefGoogle Scholar
5. Kendall, D. G. (1977) The diffusion of shape. Adv. Appl. Prob. 9, 428–430.Google Scholar
6. Kendall, D. G. and Kendall, W. S. (1980) Alignments in two-dimensional random sets of points. Adv. Appl. Prob. 12, 380–424.CrossRefGoogle Scholar
7. Kendall, D. G. (1984) Shape manifolds, procrustean metrics, and complex projective spaces. Bull. London Math. Soc. 16, 81–121.Google Scholar
8. Small, C. G. (1982) Random uniform triangles and the alignment problem. Math. Proc. Camb. Phil. Soc. 91, 315–322.Google Scholar
9. Small, C. G. (1984) A classification theorem for planar distributions based on the shape statistics of independent tetrads. Math. Proc. Camb. Phil. Soc. 96, 543–547.CrossRefGoogle Scholar