Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T00:12:35.940Z Has data issue: false hasContentIssue false
  • English
  • Français

The covariance function of the virtual waiting-time process in an M/G/1 queue

Published online by Cambridge University Press:  01 July 2016

Teunis J. Ott
Teunis J. Ott*
Affiliation:
Case Western Reserve University
*
∗Now at the University of Texas at Dallas.
Get access Rights & Permissions [Opens in a new window]

Abstract

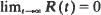Let R(t) be the covariance function of the stationary virtual waiting-time process of a stable M/G/1 queue. It is proven that if R(t) exists, i.e., if the service-times have a finite third moment, then R(t) is positive and convex on [0, ∞), with an absolutely continuous derivative R’ and a bounded, non-negative second derivative R″. Also, and R″ cannot be chosen monotone. Contrary to a finding by Beneš [1] it is proven that if and only if the service-times have a finite fourth moment.

Keywords

QUEUEING THEORYM/G/1 QUEUESVIRTUAL WAITING-TIME PROCESSESCOVARIANCE FUNCTIONS
Type
Research Article
Information
Advances in Applied Probability , Volume 9 , Issue 1 , March 1977 , pp. 158 - 168
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Beneš, V. E. (1957) On queues with Poisson arrivals. Ann. Math. Statist. 28, 670–677.CrossRefGoogle Scholar
[2] Cramèr, H. and Leadbetter, M. R. (1967) Stationary and Related Stochastic Processes. Wiley, New York.Google Scholar
[3] Feller, W. (1966) An Introduction to Probability Theory and its Applications, II. Wiley, New York.Google Scholar
[4] Keilson, J. (1963) The first passage time problem. Ann. Math. Statist. 34, 1003–1011.Google Scholar
[5] Keilson, J. (1971) On the structure of covariance functions and spectral density functions for processes reversible in time. Center for System Science Report CSS 71–03, University of Rochester, Rochester, N.Y. Google Scholar
[6] Keilson, J. and Kooharian, A. (1960) On time-dependent queueing processes. Ann. Math. Statist. 31, 104–112.Google Scholar
[7] Pakes, A. G. (1971) The correlation coefficients of the queue-lengths of some stationary single server queues. J. Austral. Math. Soc. 12, 35–46.Google Scholar
[8] Takács, L. (1962) Introduction to the Theory of Queues. Oxford University Press, New York.Google Scholar