Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T14:26:38.905Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustering of Bursts of Openings in Markov and Semi-Markov Models of Single Channel Gating

Part of: Physiological, cellular and medical topics Special processes Markov processes

Published online by Cambridge University Press:  01 July 2016

Frank Ball  and
Sue Davies
Frank Ball*
Affiliation:
The University of Nottingham
Sue Davies*
Affiliation:
The University of Nottingham
*
∗ Postal address: Department of Mathematics, University of Nottingham, University Park, Nottingham NG7 2RD, UK.
∗ Postal address: Department of Mathematics, University of Nottingham, University Park, Nottingham NG7 2RD, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

The gating mechanism of a single ion channel is usually modelled by a continuous-time Markov chain with a finite state space. The state space is partitioned into two classes, termed ‘open’ and ‘closed’, and it is possible to observe only which class the process is in. In many experiments channel openings occur in bursts. This can be modelled by partitioning the closed states further into ‘short-lived’ and ‘long-lived’ closed states, and defining a burst of openings to be a succession of open sojourns separated by closed sojourns that are entirely within the short-lived closed states. There is also evidence that bursts of openings are themselves grouped together into clusters. This clustering of bursts can be described by the ratio of the variance Var (N(t)) to the mean 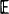[N(t)] of the number of bursts of openings commencing in (0, t]. In this paper two methods of determining Var (N(t))/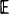[N(t)] and limt→∝ Var (N(t))/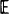[N(t)] are developed, the first via an embedded Markov renewal process and the second via an augmented continuous-time Markov chain. The theory is illustrated by a numerical study of a molecular stochastic model of the nicotinic acetylcholine receptor. Extensions to semi-Markov models of ion channel gating and the incorporation of time interval omission are briefly discussed.

Keywords

CONTINUOUS-TIME MARKOV CHAINMARKOV RENEWAL PROCESSAGGREGATED PROCESSSINGLE ION CHANNEL MODELLINGFUNDAMENTAL MATRIXSPECTRAL REPRESENTATION

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 60K15: Markov renewal processes, semi-Markov processes 92C05: Biophysics
Type
General Applied Probability
Information
Advances in Applied Probability , Volume 29 , Issue 1 , March 1997 , pp. 92 - 113
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, F. G., Davies, S. S. and Sansom, M. S. P. (1997) A sequential allosteric model for receptor-gated ion channels: modelling of single channel properties. In preparation.Google Scholar
Ball, F. G., Milne, R. K. and Yeo, G. F. (1991) Aggregated semi-Markov processes incorporating time interval omission. Adv. Appl. Prob. 23, 772–797.Google Scholar
Ball, F. G., Milne, R. K. and Yeo, G. F. (1994) Continuous-time Markov chains in a random environment, with applications to ion channel modelling. Adv. Appl. Prob. 26, 919–946.CrossRefGoogle Scholar
Ball, F. G. and Rice, J. A. (1992) Stochastic models for ion channels: introduction and bibliography. Math. Biosci. 112, 189–206.Google Scholar
Ball, F. G. and Sansom, M. S. P. (1987) Temporal clustering of ion channel openings incorporating time interval omission. IMA J. Math. Appl. Medicine Biol. 4, 333–361.Google Scholar
Bellman, R. (1970) Introduction to Matrix Analysis. 2nd edn. McGraw-Hill, New York.Google Scholar
Biggins, J. D. and Cannings, C. (1987) Markov renewal processes, counters and repeated sequences in Markov chains. Adv. Appl. Prob. 19, 521–545.Google Scholar
Çinlar, E. (1969) Markov renewal theory. Adv. Appl. Prob. 1, 123–187.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1981) On the stochastic properties of single ion channels. Proc. R. Soc. London B 211, 205–235.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1982) On the stochastic properties of bursts of single ion channel openings and of clusters of bursts. Phil. Trans. R. Soc. London B 300, 1–59.Google Scholar
Colquhoun, D. and Hawkes, A. G. (1983) The principles of stochastic interpretation of ion-channel mechanisms. In Single-Channel Recording. ed. Sakmann, B. and Neher, E.. Plenum, New York. pp. 135–175.Google Scholar
Colquhoun, D. and Sakmann, B. (1981) Fluctuations in the microsecond time range of the current through single acetylcholine receptor ion channels. Nature 294, 464–466.Google Scholar
Csenki, A. (1991) Some renewal-theoretical investigations in the theory of sojourn times in finite semi-Markov processes. J. Appl. Prob. 28, 822–832.Google Scholar
Fredkin, D. R., Montal, M. and Rice, J. A. (1985) Identification of aggregated Markovian models: application to the nicotinic acetylcholine receptor. Proc. Berkeley Conf. in Honor of Jerzy Neyman and Jack Kiefer. Vol. 1. ed. Le Cam, L. and Olshen, R.. Wadsworth, Belmont, CA. pp. 269–290.Google Scholar
Fredkin, D. R. and Rice, J. A. (1986) On aggregated Markov processes. J. Appl. Prób. 23, 208–214.Google Scholar
Hawkes, A. G. and Colquhoun, D. (1987) The effect of limited time-resolution on the observed burst kinetics of ion channels. Unpublished manuscript.Google Scholar
Hunter, J. J. (1969) On the moments of Markov renewal processes. Adv. Appl. Prob. 1, 188–210.CrossRefGoogle Scholar
Jackson, M. B. (1988) Dependence of acetylcholine receptor channel kinetics on agonist concentration in cultured mouse muscle fibres. J. Physiol. 397, 555–583.Google Scholar
Keilson, J. (1969) On the matrix renewal function for Markov renewal processes. Ann. Math. Statist. 40, 1901–1907.Google Scholar
Keilson, J. (1979) Markov Chain Models-Rarity and Exponentiality. Springer, New York.Google Scholar
Kelly, F. P. (1979) Reversibility and Stochastic Networks. Wiley, Chichester.Google Scholar
Kemeny, J. and Snell, J. (1976) Finite Markov Chains. 2nd edn. Springer, New York.Google Scholar
Koshland, D. E. Jr., Némethy, G. and Filmer, D. (1966) Comparison of experimental binding data and theoretical models in proteins containig subunits. Biochem. 5, 365–385.Google Scholar
Kshirsagar, A. M. and Gupta, Y. P. (1967) Asymptotic values of the first two moments in Markov renewal processes. Biometrika 54, 597–603.Google Scholar
Masuda, Y. and Sumita, U. (1987) Analysis of a counting process associated with a semi-Markov process: number of entries into a subset of state space. Adv. Appl. Prob. 19, 767–783.CrossRefGoogle Scholar
Pyke, R. (1961) Markov renewal processes: definitions and preliminary properties. Ann. Math. Statist. 32, 1231–1242.Google Scholar
Sakmann, B. and Neher, E. (1983) Single-Channel Recording. Plenum, New York.Google Scholar
Sakmann, B., Patlak, J. and Neher, E. (1980) Single acetylcholine-activated channels show burst-kinetics in presence of desensitizing concentrations of agonist. Nature 286, 71–73.Google Scholar