Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T16:16:09.640Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic stationarity of multichannel queues

Part of: Probability theory on algebraic and topological structures Special processes

Published online by Cambridge University Press:  01 July 2016

Władysław Szczotka
Władysław Szczotka*
Affiliation:
Wrocław University
*
∗Postal address: Mathematical Institute, Wroclaw University, Pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland.
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper deals with asymptotic stationarity of the process 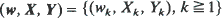where 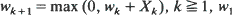is a vector in 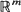with non-negative coordinates, 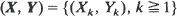is an 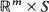-valued process, S is a separable metric space and all operations in 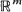are meant in the coordinate-wise sense. It is shown that a type of asymptotic stationarity of (X, Y), together with some conditions, implies the same type of asymptotic stationarity of (w, X, Y). This result is applied to analyze asymptotic stationarity of multichannel queues. It may also be used to analyze asymptotic stationarity of series of multichannel queues.

Keywords

VECTOR OF WAITING TIMESSTATIONARY REPRESENTATIONWEAK CONVERGENCESTRONG CONVERGENCECONVERGENCE IN VARIATION

MSC classification

Primary: 60K25: Queueing theory
Secondary: 60B10: Convergence of probability measures 60B12: Limit theorems for vector-valued random variables (infinite-dimensional case)
Type
Research Article
Information
Advances in Applied Probability , Volume 25 , Issue 1 , March 1993 , pp. 203 - 220
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Asmussen, S. (1987) Applied Probability and Queues. Wiley, New York.Google Scholar
[2] Berbee, H. C. P. (1979) Random Walks with Stationary Increments and Renewal Theory. Mathematisch Centrum, Amsterdam.Google Scholar
[3] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[4] Borovkov, A. A. (1972) Stochastic Processes in Queueing Theory (in Russian). Nauka, Moscow.Google Scholar
[5] Borovkov, A. A. (1980) Asymptotic Methods in Queueing Theory (in Russian). Nauka, Moscow.Google Scholar
[6] Borovkov, A. A. (1989) On the ergodicity and stability of the sequence wn + 1 =f(wn, ?n). Applications to communication networks. Theory Prob. Appl. 33, 595–611.Google Scholar
[7] Brandt, A., Lisek, B. and Franken, P. (1990) Stationary Stochastic Models. Wiley, New York.Google Scholar
[8] Breiman, L. (1968) Probability. Addison-Wesley, Reading, MA.Google Scholar
[9] Brown, J. R. (1976) Ergodic Theory and Topological Dynamics. Academic Press, New York.Google Scholar
[10] Charlot, F., Ghidouche, M. and Hamami, H. (1978) Irréductibilité et récurrence au sens de Harris des temps d'attente des files GI/G/q. Z. Wahrscheinlichkeitsth. 43, 187–203.Google Scholar
[11] Gnedenko, B. V. and Kovalenko, I. H. (1966) Introduction to Queueing Theory (in Russian). Nauk, Moscow.Google Scholar
[12] Haight, F. A. (1958) Two queues in parallel. Biometrika 45, 401–410.CrossRefGoogle Scholar
[13] Kiefer, J. and Wolfowitz, J. (1955) On the theory of queues with many servers. Trans. Amer. Math. Soc. 78, 1–18.CrossRefGoogle Scholar
[14] Kingman, J. F. (1961) Two similar queues in parallel. Ann. Math. Statist. 32, 1314–1323.CrossRefGoogle Scholar
[15] Lemoine, A. J. (1975) Queueing system with heterogeneous servers and autonomous traffic control. Operat. Res. 23, 681–686.Google Scholar
[16] Loynes, R. (1962) The stability of a queue with non-independent inter-arrival and service times. Proc. Camb. Phil. Soc. 58, 497–520.Google Scholar
[17] O'Brien, G. L. (1974) Limit theorems for sums of chain-dependent processes. J. Appl. Prob. 11, 582–587.CrossRefGoogle Scholar
[18] Oprisan, G. H. (1976) On the J–X processes. Roum. Math. Pures Appl. 21, 717–724.Google Scholar
[19] Orey, S. (1971) Lectures Notes on Limit Theorems for Markov Chain Transition Probabilities. Van Nostrand and Reinhold, London.Google Scholar
[20] Szczotka, W. (1986) Joint distribution of waiting time and queue size for single server queues. Dissertationes Math. 248.Google Scholar
[21] Szczotka, W. (1986) Stationary representation of queues I. Adv. Appl. Prob. 18, 815–848.Google Scholar
[22] Szczotka, W. (1985) Asymptotic stationarity of multichannel queues. Mathematical Institute, University of Wroclaw, Preprint No 43.Google Scholar
[23] Szczotka, W. (1990) Exponential approximation of waiting time and queue size for queues in heavy traffic. Adv. Appl. Prob. 22, 230–240.CrossRefGoogle Scholar
[24] Szczotka, W. and Kelly, F. P. (1990) Asymptotic stationarity of queues in series and the heavy traffic approximation. Ann. Prob. 18, 1232–1248.Google Scholar
[25] Whitt, W. (1970) Multiple channel queues in heavy traffic III. Random server selection. Adv. Appl. Prob. 2, 370–375.CrossRefGoogle Scholar
[26] Whitt, W. (1971) Embedded renewal processes in GI/G/a queues. J. Appl. Prob. 9, 650–658.CrossRefGoogle Scholar
[27] Whitt, W. (1982) Existence of limiting distributions in the GI/G/s queues. Math. Operat. Res. 7, 88–94.CrossRefGoogle Scholar