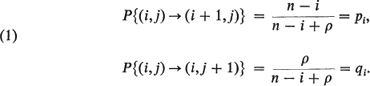Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-09T13:38:50.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic methods for problems in the mathematical theory of epidemics

Published online by Cambridge University Press:  01 July 2016

A. V. Nagaev
A. V. Nagaev*
Affiliation:
Institute of Mathematics of the Uzbek S. S. R. Academy of Sciences, Tashkent
Get access Rights & Permissions [Opens in a new window]

Extract

Let n and m be the initial numbers of susceptibles and infectives respectively in the well-known model of Bailey. The successive states of a population will be described by (i,j), where i is the number infected since the beginning of the epidemic, and j is the number removed (dead, isolated or recovered and immune) during the same period. The transition probabilities obviously are the following

Type
III. Results on the General Stochastic Epidemic
Information
Advances in Applied Probability , Volume 3 , Issue 2 , Autumn 1971 , pp. 222 - 223
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bailey, N. T. J. (1957) The Mathematical Theory of Epidemics. Griffin, London.Google Scholar
[2] Nagaev, A. N. and Startsev, A. N. (1970) Asymptotic analysis of a stochastic epidemic model. Teor. Verojat. Primen. 15, 97–105.Google Scholar