Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-09T13:19:24.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behavior of a generalization of Bailey's simple epidemic

Published online by Cambridge University Press:  01 July 2016

George H. Weiss  and
Menachem Dishon
George H. Weiss
Affiliation:
National Institutes of Health, Bethesda, Md.
Menachem Dishon
Affiliation:
Weizmann Institute of Science, Rehovot, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

It has been shown that for many epidemic models, the stochastic theory leads to essentially the same results as the deterministic theory provided that one identifies mean values with the functions calculated from the deterministic differential equations (cf. [1]). If one considers a generalization of Bailey's simple epidemic for a fixed population of size N, represented schematically by 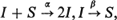where I refers to an infected, S refers to a susceptible, and α and β are appropriate rate constants, then it is evident that at time t = ∞, the expected number of infected individuals must be zero provided that β > 0. If x(t) denotes the number of infected at time t, then the deterministic model is summarized by

Type
III. Results on the General Stochastic Epidemic
Information
Advances in Applied Probability , Volume 3 , Issue 2 , Autumn 1971 , pp. 220 - 221
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Kurtz, T. G. (1969) Extension of Trotter's semigroup approximation theorems. J. Functional Anal. 3, 354–375.Google Scholar
[2] Bailey, N. T. J. (1950) A simple stochastic epidemic. Biometrika 40, 177–185.CrossRefGoogle Scholar