Published online by Cambridge University Press: 01 July 2016
The model considered here consists of n operating units which are subject to stochastic failure according to an exponential failure time distribution. These operating units are backed up by mn spare units. Failures can be of two types. With probability p (q) a failure is of type 1(2) and is sent to repair facility 1(2) for repair. Repair facility 1(2) operates as a 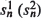 -server queue with exponential repair times having parameter μ1 (μ2). The number of units waiting for or undergoing repair at each of the two facilities is a continuous parameter Markov chain with finite state space. This paper derives limit theorems for the stationary distribution of this Markov chain as n becomes large under the assumption that
-server queue with exponential repair times having parameter μ1 (μ2). The number of units waiting for or undergoing repair at each of the two facilities is a continuous parameter Markov chain with finite state space. This paper derives limit theorems for the stationary distribution of this Markov chain as n becomes large under the assumption that 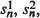 and mn grow linearly with n. These limit theorems give very useful approximations, in terms of the seven parameters characterizing the model, to a distribution that would be difficult to calculate in practice.
and mn grow linearly with n. These limit theorems give very useful approximations, in terms of the seven parameters characterizing the model, to a distribution that would be difficult to calculate in practice.