Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kertz, Robert P.
and
Rösler, Uwe
1990.
Martingales with given maxima and terminal distributions.
Israel Journal of Mathematics,
Vol. 69,
Issue. 2,
p.
173.


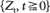 be an optional stochastic process and let
be an optional stochastic process and let 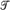 be the directed set of almost-surely-finite stopping times. If lim
be the directed set of almost-surely-finite stopping times. If lim 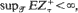 , then
, then