Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T16:11:31.877Z Has data issue: false hasContentIssue false
  • English
  • Français

An elementary renewal theorem for random compact convex sets

Part of: Special processes General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 July 2016

Ilya S. Molchanov ,
Edward Omey  and
Eugene Kozarovitzky
Ilya S. Molchanov*
Affiliation:
CWI, Amsterdam
Edward Omey*
Affiliation:
EHSAL, Brussels
Eugene Kozarovitzky*
Affiliation:
Niiravtoprom, Kiev
*
* Present address: Department of Statistics, University of Glasgow, Glasgow, G12 8QQ, UK.
** Postal address: EHSAL, Stormstraat 2, 1000 Brussels, Belgium.
*** Postal address: Niiravtoprom, Dept. PMO, Predslavinskaja 28, 252145 Kiev, Ukraine.
Get access Rights & Permissions [Opens in a new window]

Abstract

A set-valued analog of the elementary renewal theorem for Minkowski sums of random closed sets is considered. The corresponding renewal function is defined as 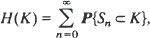where 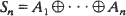are Minkowski (element-wise) sums of i.i.d. random compact convex sets. In this paper we determine the limit of H(tK)/t as t tends to infinity. For K containing the origin as an interior point, 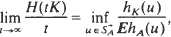where hK(u) is the support function of K and 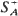is the set of all unit vectors u with EhA(u) > 0. Other set-valued generalizations of the renewal function are also suggested.

Keywords

AUMANN EXPECTATIONMINKOWSKI ADDITIONRENEWAL FUNCTION

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry 60K05: Renewal theory
Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 27 , Issue 4 , December 1995 , pp. 931 - 942
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Supported in part by the Alexander von Humboldt-Stiftung, Bonn, Germany.

References

Artstein, Z. and Vitale, R. A. (1975) A strong law of large numbers for random compact sets. Ann. Prob. 3, 879–882.CrossRefGoogle Scholar
Aumann, R. J. (1965) Integrals of set-valued functions. J. Math. Anal. Appl. 12, 1–12.CrossRefGoogle Scholar
Bickel, J. and Yahav, J. A. (1965) Renewal theory in the plane. Ann. Math. Stat. 36, 946–955.CrossRefGoogle Scholar
Cressie, N. (1979) A central limit theorem for random sets. Z. Wahrscheinlichkeitsth. 49, 37–47.CrossRefGoogle Scholar
Gafurov, M. U. (1980) On the first exit time of a multidimensional random walk from expanding sets. Sov. Math. Dokl. 22, 492–493.Google Scholar
Gine, E., Hahn, M. G. and Zinn, J. (1983) Limit theorems for random sets: application of probability in Banach space results. In Lecture Notes in Mathematics 990, pp. 112–135. Springer-Verlag, Berlin.Google Scholar
Gut, A. (1988) Stopped Random Walks: Limit Theorems and Applications. Springer-Verlag, New York.Google Scholar
Hunter, J. J. (1974) Renewal theory in two dimensions: basic results. Adv. Appl. Prob. 6, 379–391.Google Scholar
Johns, M. V. (1957) Non-parametric empirical Bayes procedures. Ann. Math. Stat. 28, 649–669.CrossRefGoogle Scholar
Lai, T. L. (1975) On uniform integrability in renewal theory. Bull. Inst. Math. Acad. Sinica 3, 99–105.Google Scholar
Lyashenko, N. N. (1982) Limit theorems for sum of independent compact random subsets. J. Soviet Math. 20, 2187–2196.CrossRefGoogle Scholar
Lyashenko, N. N. (1983) Statistics of random compacts in the Euclidean space. J. Soviet Math. 21, 76–92.CrossRefGoogle Scholar
Matheron, G. (1975) Random Sets and Integral Geometry. Wiley, New York.Google Scholar
Molchanov, I. S. (1983) A generalization of the Choquet theorem for random sets with a given class of realizations. Theor. Veroyatnost. i Matem. Statist. 28 86–93. English translation in: Theory Prob. Math. Statist. (1984) 28, 99-106.Google Scholar
Nagaev, A. V. (1979) Renewal theorems in d. Theory Prob. Appl. 34, 572–581.Google Scholar
Omey, E. (1989) Multivariate Regular Variation and Applications in Probability Theory. EHSAL, Eclectica N 74, Brussel.Google Scholar
Puri, M. L. and Ralescu, D. A. (1985) Limit theorems for random compact sets in Banach space. Math. Proc. Camb. Phil. Soc. 97, 151–158.CrossRefGoogle Scholar
Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press.Google Scholar
Smith, W. R. (1964) On the elementary renewal theorem for non-identically distributed variables. Pacific J. Math. 14, 673–700.Google Scholar
Stoyan, D., Kendall, W. S. and Mecke, J. (1987) Stochastic Geometry and Its Applications. Akademie-Verlag, Berlin/Wiley, Chichester.Google Scholar
Vitale, R. A. (1983) Some developments in the theory of random sets. Bull. Int. Statist. Inst. 50, 863–871.Google Scholar
Vitale, R. A. (1984) On Gaussian random sets. In Stochastic Geometry, Geometric Statistics, Stereology , eds. Ambartzumian, R. V. and Weil, W., pp. 222–224. Teubner, Stuttgart.Google Scholar
Vitale, R. A. (1988) An alternate formulation of mean value for random geometric figures. J. Microscopy 151, 197–204.Google Scholar
Weil, W. (1982) An application of the central limit theorem for Banach-space-valued random variables to the theory of random sets. Z. Wahrscheinlichkeitsth. 60, 203–208.CrossRefGoogle Scholar