Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T23:57:26.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Almost sure limit sets of random samples in ℝd

Published online by Cambridge University Press:  01 July 2016

Richard A. Davis ,
Edward Mulrow  and
Sidney I. Resnick
Richard A. Davis*
Affiliation:
Colorado State University
Edward Mulrow*
Affiliation:
Southern Illinois University
Sidney I. Resnick*
Affiliation:
Cornell University
*
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, USA.
∗∗Postal address: Department of Mathematics, Southern Illinois University, Carbondale, IL 62910, USA.
∗∗∗Postal address: OR/IE, Upson Hall, Cornell University, Ithaca, NY 14853, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

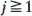If {Xj, } is a sequence of i.i.d. random vectors in 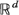, when do there exist scaling constants bn > 0 such that the sequence of random sets 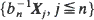converges almost surely in the space of compact subsets of 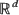to a limit set? A multivariate regular variation condition on a properly defined distribution tail guarantees the almost sure convergence but without certain regularity conditions surprises can occur. When a density exists, an exponential form of regular variation plus some regularity guarantees the convergence.

Keywords

RANDOM SETSMULTIVARIATE REGULAR VARIATIONALMOST SURE CONVERGENCEHAUSDORFF METRICCONVEX HULL
Type
Research Article
Information
Advances in Applied Probability , Volume 20 , Issue 3 , September 1988 , pp. 573 - 599
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Support gratefully acknowledged from NSF Grant DMS 85–01763 at Colorado State University.

References

Balkema, A., and Resnick, S. (1977) Max-infinite divisibility. J. Appl. Prob. 14, 309–319.Google Scholar
Barndorff-Nielsen, O. (1963) On the limit behavior of extreme order statistics. Ann. Math. Statist. 34, 992–1002.CrossRefGoogle Scholar
Barnett, V. (1976) The ordering of multivariate data. J.R. Statist. Soc. A 139, 318–354.Google Scholar
Bingham, N., Goldie, C., and Teugels, J. (1987) Regular Variation. Encyclopedia of Mathematics and its Applications, Vol. 27, Cambridge University Press.Google Scholar
Davis, R., Marengo, J. and Resnick, S. (1985) Extremal properties of a class of multivariate moving averages. Proc. 45th Session ISI, 26(2), 1–14.Google Scholar
Davis, R., Mulrow, E. and Resnick, S. (1987) The convex hull of a random sample in ℝ2 . Stochastic Models 3, 1–29.Google Scholar
Eddy, W. F. (1982) Convex hull peelings. COMPSAT 1982—Part 1: Proceedings in Computational Statistics, 42–47, Physica-Verlag, Vienna.Google Scholar
Eddy, W. F. (1983) Set-valued orderings for bivariate data. Technical Report No. 281, Dept. of Statistics, Carnegie-Mellon University.Google Scholar
Fisher, L. (1966) The convex hull of a sample. Bull. Amer. Math. Soc. 72, 555–558.Google Scholar
Fisher, L. (1969) Limiting sets and convex hulls of samples from product measures. Ann. Math. Statist. 40, 1824–1832.Google Scholar
Geoffroy, J. (1961) Localisation asymptotique du polyèdre d'appui d'un échantillon laplacien à k dimensions. Publ. Inst. Statist. Univ. Paris, X, 212–228.Google Scholar
Haan, L. De (1970) On Regular Variation and its Application to the Weak Convergence of Sample Extremes. Mathematical Centre Tract 32, Mathematics Centre, Amsterdam.Google Scholar
Haan, L. De and Omey, E. (1983) Integrals and derivatives of regularly varying functions in ℝ d and domains of attraction of stable distributions II. Stoch. Proc. Appl. 16, 157–170.Google Scholar
Haan, L. De and Resnick, S. (1979) Derivatives of regularly varying functions in ℝ d and domains of attraction of stable distributions. Stoc. Proc. Appl. 8, 349–355.Google Scholar
Haan, L. De and Resnick, S. (1987) On regular variation of probability densities. Stoch. Proc. Appl. 25, 83–93.CrossRefGoogle Scholar
Lay, S. R. (1982) Convex Sets and their Applications. Wiley, New York.Google Scholar
Macdonald, D. W., Ball, F. G., and Hough, N. G. (1980) The evaluation of home range and configuration using radio tracking data. In A Handbook on Biotelemetry and Radio Tracking, ed. MacDonald, D. W. and Amlaner, C. J.: Pergamon Press, Oxford.Google Scholar
Matheron, G. (1975) Random Sets and Integral Geometry. Wiley, New York.Google Scholar
Moore, M. (1984) On the estimation of a convex set. Ann. Statist. 12, 1090–1099.Google Scholar
Resnick, S. I. (1986) Point processes, regular variation and weak convergence. Adv. Appl. Prob. 18, 66–138.Google Scholar
Resnick, S. I. (1987) Extreme Values, Point Processes and Regular Variation. Springer-Verlag, New York.Google Scholar
Resnick, S. and Tomkins, R. (1973) Almost sure stability of maxima. J. Appl. Prob. 10, 387–401.Google Scholar
Ripley, B. D. and Rasson, J. P. (1977) Finding the edge of a Poisson forest. J. Appl. Prob. 14, 483–491.Google Scholar
Stam, A. J. (1977) Regular variation in R d + and the Abel–Tauber theorem. Reprint, Mathematisch Institut, Rijksuniversiteit Groningen.Google Scholar