Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T18:53:27.836Z Has data issue: false hasContentIssue false
  • English
  • Français

A Convex-Splitting Scheme for a Diffuse Interface Model with Peng-Robinson Equation of State

Part of: Error analysis and interval analysis Partial differential equations, initial value and time-dependent initial-boundary value problems

Published online by Cambridge University Press:  11 July 2017

Qiujin Peng
Qiujin Peng*
Affiliation:
Institute for Mathematical Sciences, Renmin University of China, No. 59 Zhongguancun Street, Haidian District, Beijing 100872, China
*
*Corresponding author. Email:[email protected] (Q. J. Peng)
Get access

Abstract

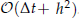We present a convex-splitting scheme for the fourth order parabolic equation derived from a diffuse interface model with Peng-Robinson equation of state for pure substance. The semi-implicit scheme is proven to be uniquely solvable, mass conservative, unconditionally energy stable and L∞ convergent with the order of . The numerical results verify the effectiveness of the proposed algorithm and also show good agreement of the numerical solution with laboratory experimental results.

Keywords

Diffuse interface modelfourth order parabolic equationconvex-splitting schemeconvergence

MSC classification

Secondary: 65M06: Finite difference methods 65M12: Stability and convergence of numerical methods 65G99: None of the above, but in this section
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 9 , Issue 5 , October 2017 , pp. 1162 - 1188
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Anderson, D., McFadden, G. B. and Wheeler, A., Diffuse-interface methods in fluid mechanics, Ann. Rev. Fluid Mech., 30 (1998), pp. 139–165.Google Scholar
[2] Baskaran, A., Lowengrub, J. S., Wang, C. and Wise, S. M., Convergence analysis of a second order convex splitting scheme for the modified phase field crystal equation, SIAM J. Numer. Anal., 51 (2013), pp. 2851–2873.Google Scholar
[3] Cahn, J. W. and Hilliard, J. E., Free energy of a nonuniform system I. Interfacial free energy, J. Chem. Phys., 28 (1958), pp. 258–267.Google Scholar
[4] Cahn, J. W., Free energy of a nonuniform system II. Thermodynamic basis, J. Chem. Phys., 30 (1959), pp. 1121–1124.Google Scholar
[5] Cahn, J. W., On spinodal decomposition, Acta Metallurgica, 9 (1961), pp. 795–801.Google Scholar
[6] Chen, W., Conde, S., Wang, C., Wang, X. and Wise, S., A linear energy stable scheme for a thin film model without slope selection, J. Sci. Comput., 52 (2012), pp. 546–562.Google Scholar
[7] Eyre, D. J., Unconditionally gradient stable time marching the Cahn–Hilliard equation, in Bullard, J. W., Kalia, R., Stoneham, M. and Chen, L. Q., (eds.) Computational and Mathematical Models of Microstructural Evolution, 53 (1998), pp. 1686–1712.Google Scholar
[8] Firoozabadi, A., Thermodynamics of Hydrocarbon Reservoirs, McGraw-Hill, New York, 1999.Google Scholar
[9] Gu, S., Zhang, H. and Zhang, Z., An energy-stable finite-difference scheme for the binary fluid-surfactant system, J. Comput. Phys., 270 (2014), pp. 416–431.Google Scholar
[10] Guo, J., Wang, C., Wise, S. M. and Yue, X., An H2 convergence of a second-order convex-splitting, finite difference scheme for the three-dimensional Cahn-Hilliard equation, Commun. Math. Sci., 14(2) (2016), pp. 489–515.Google Scholar
[11] Hu, Z., Wise, S. M., Wang, C. and Lowengrub, J. S., Stable and efficient finite-difference nonlinear-multigrid schemes for the phase field crystal equation, J. Comput. Phys., 228 (2009), pp. 5323–5339.Google Scholar
[12] Kou, J. and Sun, S., An adaptive finite element method for simulating surface tension with the gradient theory of fluid interfaces, J. Comput. Appl. Math., 255 (2014), pp. 593–604.Google Scholar
[13] Kou, J. and Sun, S., Unconditionally stable methods for simulating multi-component two-phase interface models with Peng-Robinson equation of state and various boundary conditions, J. Comput. Appl. Math., (2015).Google Scholar
[14] Kou, J., Sun, S. and Wang, X., Efficient numerical methods for simulating surface tension of multi-component mixtures with the gradient theory of fluid interfaces, Comput. Methods Appl. Mech. Eng., 292 (2015), pp. 92–106.Google Scholar
[15] Li, J., Sun, Z. Z. and Zhao, X., A three level linearized compact difference scheme for the Cahn-Hilliard equation, Sci. China Math., 55(4) (2012), pp. 805–826.Google Scholar
[16] Li, D. and Qiao, Z., On second order semi-implicit Fourier spectral methods for 2D Cahn-Hilliard equations, J. Sci. Comput., (2016), DOI: 10.1007/s10915-016-0251-4.Google Scholar
[17] Li, D., Qiao, Z. and Tang, T., Characterizing the stabilization size for semi-implicit Fourier-Spetral method to phase field equations, SIAM J. Numer. Anal., 54 (2016), pp. 1653–1681.Google Scholar
[18] Lin, H. and Duan, Y., Surface tension measurements of propane (r–290) and isobutane (r–600a) from (253 to 333)K, J. Chem. Eng. Data, 48 (2003), pp. 1360–1363.Google Scholar
[19] Liao, H. and Sun, Z., Maximum norm error bounds of ADI and compact ADI methods for solving parabolic equations, Numer. Methods Partial Differential Equations, 26 (2010), pp. 37–60.Google Scholar
[20] Peng, D. Y. and Robinson, D. B., A new two-constant equation of state, Industrial and Engineering Chemistry Fundamentals, 15(1) (1976), pp. 59–64.Google Scholar
[21] Peng, Q., Qiao, Z. and Sun, S., Stability and convergence analysis of second-order schemes for a diffuse interface model with Peng-Robinson equation of state, J. Comput. Math., doi:10.4208/jcm.1611-m2016-0623.Google Scholar
[22] Qiao, Z., Sun, Z. and Zhang, Z., The stability and convergence of two linearized finite difference schemes for the nonlinear epitaxial growth model, Numer. Methods Partial Differential Equations, 28(6) (2012), pp. 1893–1915.Google Scholar
[23] Qiao, Z. and Sun, S., Two-phase fluid simulation using a diffuse interface model with Peng–Robinson equation of state, SIAM J. Sci. Comput., 36(4) (2014), pp. B708–B728.Google Scholar
[24] Qiao, Z., Sun, Z. and Zhang, Z., Stability and convergence of second-order schemes for the nonlinear epitaxial growth model without slope selection. Math. Comput., 84 (2015), pp. 653–674.Google Scholar
[25] Robinson, D. B., Peng, D. and Chung, S. Y., The development of the Peng-Robinson equation and its application to phase equilibrium in a system containing methanol, Fluid Phase Equilibria, 24 (1985), pp. 25–41.Google Scholar
[26] Shen, J., Wang, C., Wang, X. and Wise, S. M., Second–order convex splitting schemes for gradient flows with Ehrlich-Schwoebel type energy: application to thin film epitaxy, SIAM J. Numer. Anal., 50 (2012), pp. 105–125.Google Scholar
[27] Shen, J. and Yang, X., Numerical approximations of Allen–Cahn and Cahn–Hilliard equations, Discrete Contin. Dyn. Syst. Ser. A, 28 (2010), pp. 1669–1691.Google Scholar
[28] Sun, Z., A second–order accurate linearized difference scheme for the two–dimensional Cahn–Hilliard equation, Math. Comput., 64(212) (1995), pp. 1463–1471.Google Scholar
[29] Van Der Waals, J. D., “verhandel. konink. akad. weten. amsterdam” vol. 1 no. 8 (dutch) 1893, translation of van der Waals, J. D. (The thermodynamic theory of capillarity under the hypothesis of a continuous density variation), J. Stat. Phys., 1979.Google Scholar
[30] Vignal, P., Dalcin, L., Brown, D. L., Collier, N. and Calo, V. M., An energy-stable convex splitting for the phase-field crystal equation, Comput. Struct., 158 (2015), pp. 355–368.Google Scholar
[31] Wang, C., Wang, X. and Wise, S. M., Unconditionally stable schemes for equations of thin film epitaxy, Discrete Contin. Dyn. Syst. Ser. A, 28 (2010), pp. 405–423.Google Scholar
[32] Wang, C. and Wise, S. M, An energy stable and convergent finite-difference scheme for the modified phase field crystal equation, SIAM J. Numer. Anal., 49 (2011), pp. 945–969.Google Scholar
[33] Wise, S. M., Wang, C. and Lowengrub, J. S., An energy-stable and convergent finite-difference scheme for the phase field crystal equation, SIAM J. Numer. Anal., 47 (2009), pp. 2269–2288.Google Scholar
[34] Xu, C. and Tang, T., Stability analysis of large time-stepping methods for epitaxial growth models, SIAM J. Numer. Anal., 44 (2006), pp. 1759–1779.Google Scholar