Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T08:20:02.837Z Has data issue: false hasContentIssue false
  • English
  • Français

The Collocation Method and the Splitting Extrapolation for the First Kind of Boundary Integral Equations on Polygonal Regions

Published online by Cambridge University Press:  03 June 2015

Li Wang
Li Wang*
Affiliation:
Civil Aviation Flight University of China, Guanghan 618307, China
*
*Corresponding author. Email: [email protected]
Get access

Abstract

In this paper, the collocation methods are used to solve the boundary integral equations of the first kind on the polygon. By means of Sidi’s periodic transformation and domain decomposition, the errors are proved to possess the multi-parameter asymptotic expansion at the interior point with the powers 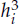(i = 1,...,d), which means that the approximations of higher accuracy and a posteriori estimation of the errors can be obtained by splitting extrapolations. Numerical experiments are carried out to show that the methods are very efficient.

Keywords

65R10Splitting extrapolationboundary integral equation of the first kind on polygoncollocation methodposteriori estimation
Type
Research Article
Information
Advances in Applied Mathematics and Mechanics , Volume 4 , Issue 5 , October 2012 , pp. 603 - 616
Copyright
Copyright © Global-Science Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Sloan, I. and Spence, A., The Galerkin method for integral equations of the first kind with Logarithmic kernel, IMA J. Numer. Anal., 8(1988), pp. 105–122.Google Scholar
[2]Yan, Y., The collocation method for first-kind boundary integral equation on polygonal regions, Math. Comp., 189(54) (1990), pp. 139–154.CrossRefGoogle Scholar
[3]Yan, Y. and Sloan, I., Mesh grading for Integral equation of the first-Kind with logarithmic kernel, SIAM J. Neumer. Appl., 26 (1989), pp. 574–578.CrossRefGoogle Scholar
[4]Lu, T. and Huang, J., Quadrature methods with high accuracy and extrapolation for solving boundary integral equations of the first kind, Math. Numer. Sin., 22(1) (2000), pp. 59–72.Google Scholar
[5]Sidi, A., A new variable transformation for numerical integration, in: Numerical Integration IV, I. S. Num. Math, 112 (1993), pp. 359–373.Google Scholar
[6]Liem, C. B., Shih, T. M. and Lu, T., Splitting Extrapolation Methods, World Scientific Publishing Singapore, 1995.Google Scholar