Published online by Cambridge University Press: 09 June 2022
Schwarz methods use a decomposition of the computational domain into subdomains and need to impose boundary conditions on the subdomain boundaries. In domain truncation one restricts the unbounded domain to a bounded computational domain and must also put boundary conditions on the computational domain boundaries. In both fields there are vast bodies of literature and research is very active and ongoing. It turns out to be fruitful to think of the domain decomposition in Schwarz methods as a truncation of the domain onto subdomains. Seminal precursors of this fundamental idea are papers by Hagstrom, Tewarson and Jazcilevich (1988), Després (1990) and Lions (1990). The first truly optimal Schwarz method that converges in a finite number of steps was proposed by Nataf (1993), and used precisely transparent boundary conditions as transmission conditions between subdomains. Approximating these transparent boundary conditions for fast convergence of Schwarz methods led to the development of optimized Schwarz methods – a name that has become common for Schwarz methods based on domain truncation. Compared to classical Schwarz methods, which use simple Dirichlet transmission conditions and have been successfully used in a wide range of applications, optimized Schwarz methods are much less well understood, mainly due to their more sophisticated transmission conditions.
A key application of Schwarz methods with such sophisticated transmission conditions turned out to be time-harmonic wave propagation problems, because classical Schwarz methods simply do not work in this case. The past decade has given us many new Schwarz methods based on domain truncation. One review from an algorithmic perspective (Gander and Zhang 2019) showed the equivalence of many of these new methods to optimized Schwarz methods. The analysis of optimized Schwarz methods, however, is lagging behind their algorithmic development. The general abstract Schwarz framework cannot be used for the analysis of these methods, and thus there are many open theoretical questions about their convergence. Just as for practical multigrid methods, Fourier analysis has been instrumental for understanding the convergence of optimized Schwarz methods and for tuning their transmission conditions. Similar to local Fourier mode analysis in multigrid, the unbounded two-subdomain case is used as a model for Fourier analysis of optimized Schwarz methods due to its simplicity. Many aspects of the actual situation, e.g. boundary conditions of the original problem and the number of subdomains, were thus neglected in the unbounded two-subdomain analysis. While this gave important insight, new phenomena beyond the unbounded two-subdomain models were discovered.
This present situation is the motivation for our survey: to give a comprehensive review and precise exploration of convergence behaviours of optimized Schwarz methods based on Fourier analysis, taking into account the original boundary conditions, many-subdomain decompositions and layered media. We consider as our model problem the operator
$-\Delta + \eta $
 in the diffusive case
$\eta>0$
in the diffusive case
$\eta>0$
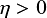 (screened Laplace equation) or the oscillatory case
$\eta <0$
(screened Laplace equation) or the oscillatory case
$\eta <0$
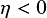 (Helmholtz equation), in order to show the fundamental difference in behaviour of Schwarz solvers for these problems. The transmission conditions we study include the lowest-order absorbing conditions (Robin), and also more advanced perfectly matched layers (PMLs), both developed first for domain truncation. Our intensive work over the last two years on this review has led to several new results presented here for the first time: in the bounded two-subdomain analysis for the Helmholtz equation, we see strong influence of the original boundary conditions imposed on the global problem on the convergence factor of the Schwarz methods, and the asymptotic convergence factors with small overlap can differ from the unbounded two-subdomain analysis. In the many-subdomain analysis, we find the scaling with the number of subdomains, e.g. when the subdomain size is fixed, robust convergence of the double-sweep Schwarz method for the free-space wave problem, either with fixed overlap and zeroth-order Taylor conditions or with a logarithmically growing PML, and we find that Schwarz methods with PMLs work like smoothers that converge faster for higher Fourier frequencies; in particular, for the free-space wave problem, plane waves (in the error) passing through interfaces at a right angle converge more slowly. In addition to our main focus on analysis in Sections 2 and 3, we start in Section 1 with an expository historical introduction to Schwarz methods, and in Section 4 we give a brief interpretation of the recently proposed optimal Schwarz methods for decompositions with cross-points from the viewpoint of transmission conditions. We conclude in Section 5 with a summary of open research problems. In Appendix A we provide a Matlab program for a block LU form of an optimal Schwarz method with cross-points, and in Appendix B we give the Maple program for the two-subdomain Fourier analysis.
(Helmholtz equation), in order to show the fundamental difference in behaviour of Schwarz solvers for these problems. The transmission conditions we study include the lowest-order absorbing conditions (Robin), and also more advanced perfectly matched layers (PMLs), both developed first for domain truncation. Our intensive work over the last two years on this review has led to several new results presented here for the first time: in the bounded two-subdomain analysis for the Helmholtz equation, we see strong influence of the original boundary conditions imposed on the global problem on the convergence factor of the Schwarz methods, and the asymptotic convergence factors with small overlap can differ from the unbounded two-subdomain analysis. In the many-subdomain analysis, we find the scaling with the number of subdomains, e.g. when the subdomain size is fixed, robust convergence of the double-sweep Schwarz method for the free-space wave problem, either with fixed overlap and zeroth-order Taylor conditions or with a logarithmically growing PML, and we find that Schwarz methods with PMLs work like smoothers that converge faster for higher Fourier frequencies; in particular, for the free-space wave problem, plane waves (in the error) passing through interfaces at a right angle converge more slowly. In addition to our main focus on analysis in Sections 2 and 3, we start in Section 1 with an expository historical introduction to Schwarz methods, and in Section 4 we give a brief interpretation of the recently proposed optimal Schwarz methods for decompositions with cross-points from the viewpoint of transmission conditions. We conclude in Section 5 with a summary of open research problems. In Appendix A we provide a Matlab program for a block LU form of an optimal Schwarz method with cross-points, and in Appendix B we give the Maple program for the two-subdomain Fourier analysis.