The recent work of Siegelman & Young (Proc. Natl Acad. Sci. USA, vol. 120, issue 44, 2023, e2308018120) revealed two extreme states reached by the evolution of unforced and weakly damped two-dimensional turbulence above random rough topography, separated by a critical kinetic energy 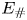 $E_\#$. The low- and high-energy solutions correspond to topographically locked and roaming vortices, surrounded by non-uniform and homogeneous background potential vorticity (PV), respectively. However, we found that these phenomena are restricted to the particular intermediate length scale where the energy was initially injected into the system. Through simulations initialized by injecting the energy at larger and smaller length scales, we found that the long-term state of topographic turbulence is also dependent on the initial length scale and thus the initial enstrophy. If the initial length scale is comparable to the domain size, the long-term flow field resembles the minimum-enstrophy state proposed by Bretherton & Haidvogel (J. Fluid Mech., vol. 78, issue 1, 1976, pp. 129–154), with very few topographically locked vortices; the long-term enstrophy is quite close to the minimum value, especially when the energy is no larger than
$E_\#$. The low- and high-energy solutions correspond to topographically locked and roaming vortices, surrounded by non-uniform and homogeneous background potential vorticity (PV), respectively. However, we found that these phenomena are restricted to the particular intermediate length scale where the energy was initially injected into the system. Through simulations initialized by injecting the energy at larger and smaller length scales, we found that the long-term state of topographic turbulence is also dependent on the initial length scale and thus the initial enstrophy. If the initial length scale is comparable to the domain size, the long-term flow field resembles the minimum-enstrophy state proposed by Bretherton & Haidvogel (J. Fluid Mech., vol. 78, issue 1, 1976, pp. 129–154), with very few topographically locked vortices; the long-term enstrophy is quite close to the minimum value, especially when the energy is no larger than 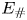 $E_\#$. As the initial length scale becomes smaller, more vortices nucleate and become more mobile; the long-term enstrophy increasingly deviates from the minimum value. Simultaneously, the background PV tends to homogenization, even if the energy is below
$E_\#$. As the initial length scale becomes smaller, more vortices nucleate and become more mobile; the long-term enstrophy increasingly deviates from the minimum value. Simultaneously, the background PV tends to homogenization, even if the energy is below 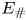 $E_\#$. These results complement the phenomenology of topographic turbulence documented by Siegelman & Young, by showing that the minimum-enstrophy and background PV homogenization states can be adequately approached by large- and small-scale initial fields, respectively, with relatively arbitrary energy.
$E_\#$. These results complement the phenomenology of topographic turbulence documented by Siegelman & Young, by showing that the minimum-enstrophy and background PV homogenization states can be adequately approached by large- and small-scale initial fields, respectively, with relatively arbitrary energy.
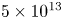 $5\times 10^{13}$
$5\times 10^{13}$
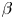 $\beta$-plane zonal jets
$\beta$-plane zonal jets