Let 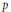 $p$ be an odd prime number,
$p$ be an odd prime number, 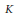 $K$ a
$K$ a 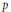 $p$-adic field of degree
$p$-adic field of degree 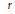 $r$ over
$r$ over 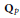 ${{\mathbf{Q}}_{p}}$,
${{\mathbf{Q}}_{p}}$, 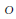 $O$ the ring of integers in
$O$ the ring of integers in 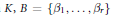 $K,\,B\,=\,\{{{\beta }_{1}},\ldots .{{\beta }_{r}}\}$ an integral basis of
$K,\,B\,=\,\{{{\beta }_{1}},\ldots .{{\beta }_{r}}\}$ an integral basis of 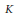 $K$ over
$K$ over 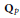 ${{\mathbf{Q}}_{p}}$,
${{\mathbf{Q}}_{p}}$, 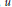 $u$ a unit in
$u$ a unit in 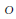 $O$ and consider sets of the form
$O$ and consider sets of the form 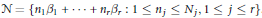 $N\,=\,\{{{n}_{1}}{{\beta }_{1}}\,+\ldots +\,{{n}_{r}}{{\beta }_{r}}\,:\,1\,\le \,{{n}_{j}}\,\le \,{{N}_{j}},\,1\,\le \,j\,\le \,r\}$. We show under certain growth conditions that the pair correlation of
$N\,=\,\{{{n}_{1}}{{\beta }_{1}}\,+\ldots +\,{{n}_{r}}{{\beta }_{r}}\,:\,1\,\le \,{{n}_{j}}\,\le \,{{N}_{j}},\,1\,\le \,j\,\le \,r\}$. We show under certain growth conditions that the pair correlation of 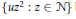 $\{u{{z}^{2}}\,:\,z\,\in N\}$ becomes Poissonian.
$\{u{{z}^{2}}\,:\,z\,\in N\}$ becomes Poissonian.
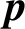 $\boldsymbol {p}$
-ADIC ELLIPTIC TRANSCENDENCE
$\boldsymbol {p}$
-ADIC ELLIPTIC TRANSCENDENCE
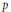 $p$-Adic Fields
$p$-Adic Fields
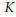 $K$-Theory Galois Module Structure Invariants
$K$-Theory Galois Module Structure Invariants