Use is made of the extraordinary-mode eigenvalue equation to investigate detailed properties of the magneteron instability for relativistic nonneutral electron flow in a cylindrical high-voltage diode with cathode located at r = a and the anode located at r = b. The model is based on the cold-fluid-Maxwell equations including the full influence of self-field and cylindrical effects. The equilibrium radial electric field Er (r)êr and axial magnetic field Bz (r)êz induce an azimuthal flow of electrons with angular velocity ωb(r) = Vθb (r)/r. The stability analysis assumes flute perturbations with extraordinary-mode polarization. The equilibrium radial electric field is specified by Er (r) = const, sinh k (r − a) within the electron layer (a ≤ r ≤ rb), and emphasis is placed on calculating equilibrium and stability behavior in a parameter regime characteristic of the PBFA-II diode experiments. In particular, voltages in the range 10 MV to 14·75 MV are considered, assuming a = 12 cm, b = 15 cm, and normalized layer thickness Δb = (rb − a)/(b − a) ranging from Δb = 0·3 to Δb = 0·6. At the high voltages characteristic of PBFA-II operation, a moderately strong applied magnetic field B0 is required to assure magnetic insulation of the layer electrons from the anode. Here, B0 is the magnetic field in the vacuum region rb < r ≤ b. Correspondingly, the value of normalized density  is typically small. Here, ωc0 = eB0/mc, and ωp0 is the plasma frequency at the cathode. As a general remark, for fixed values of the geometric factors Δb, b − a, etc., it is found that there is a sensitive dependence of the magnetron instability growth rate on the relativistic flow velocity as measured by
is typically small. Here, ωc0 = eB0/mc, and ωp0 is the plasma frequency at the cathode. As a general remark, for fixed values of the geometric factors Δb, b − a, etc., it is found that there is a sensitive dependence of the magnetron instability growth rate on the relativistic flow velocity as measured by 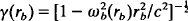 , with higher values of γ(rb) favoring stronger growth. Typical maximum growth rates are in the range of a few to several percent of ωc0.
, with higher values of γ(rb) favoring stronger growth. Typical maximum growth rates are in the range of a few to several percent of ωc0.