The notions of recursively saturated and resplendent models grew out of the study of admissible sets with urelements and admissible fragments of L
ω1ω, but, when applied to ordinary first order model theory, give us new tools for research and exposition. We will discuss their history in §3.
The notion of saturated model has proven to be important in model theory. Its most important property for applications is that if 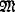 ,
, 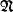 are saturated and of the same cardinality then
are saturated and of the same cardinality then 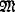 =
= 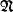 iff
iff 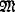 ≅
≅ 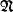 . See, e.g., Chang-Keisler [3]. The main drawback is that saturated models exist only under unusual assumptions of set theory. For example, if 2κ = κ+ then every theory T of L has a saturated model of power κ+. (Similarly, if κ is strongly inaccessible, then every T has a saturated model of power κ.) On the other hand, a theory T like Peano arithmetic, with
. See, e.g., Chang-Keisler [3]. The main drawback is that saturated models exist only under unusual assumptions of set theory. For example, if 2κ = κ+ then every theory T of L has a saturated model of power κ+. (Similarly, if κ is strongly inaccessible, then every T has a saturated model of power κ.) On the other hand, a theory T like Peano arithmetic, with 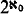 types, cannot have a saturated model in any power κ with ω ≤ κ ≤
types, cannot have a saturated model in any power κ with ω ≤ κ ≤ 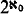 .
.
One method for circumventing these problems of existence (or rather non-existence) is the use of “special” models (cf. [3]). If κ = Σλ<κ2λ, κ < ω, then every theory T of L has a special model of power κ. Such cardinals are large and, themselves, rather special. There are definite aesthetic objections to the use of these large, singular models to prove results about first order logic.