The set theory AFC was introduced by Perlis in [2] and he noted that it both includes and is stronger than Ackermann's set theory. We shall give a relative consistency result for AFC.
AFC is obtained from Ackermann's set theory (see [2]) by replacing Ackermann's set existence schema with the schema
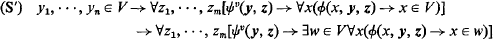
(where ϕ, ψ, are ∈-formulae, x is not in ψ, w is not in ϕ, y is y
1, …, yn, z is z
1, …, zm
and all free variables are shown) and adding the axiom of choice for sets. Following [1], we say that λ is invisible in Rκ if λ < κ and we have
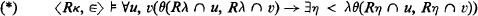
holding for every ∈-formula θ which has exactly two free variables and does not involve u or υ. The existence of a Ramsey cardinal implies the existence of cardinals λ and κ with λ invisible in Rκ, and Theorem 1.13 of [1] gives some further indications about the relative strength of the notion of invisibility.
Theorem. If there are cardinals λ and κ with λ invisible in Rκ, then AFC is consistent.
Proof. Suppose that λ is invisible in Rκ and we will show that 〈Rκ, Rλ, ∈〉 ⊧ AFC (Rλ being the interpretation of V, of course).