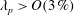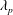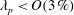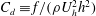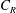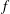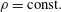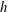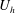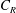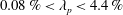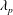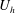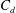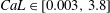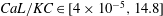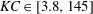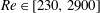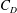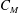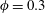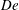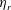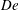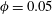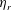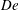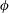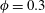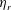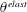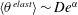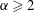We present a numerical study of the rheology of a two-fluid emulsion in dilute and semidilute conditions. The analysis is performed for different capillary numbers, volume fractions and viscosity ratios under the assumption of negligible inertia and zero buoyancy force. The effective viscosity of the system increases for low values of the volume fraction and decreases for higher values, with a maximum for approximately 20 % concentration of the disperse phase. When the dispersed fluid has lower viscosity, the normalised effective viscosity becomes smaller than 1 for high enough volume fractions. To single out the effect of droplet coalescence on the rheology of the emulsion we introduce an Eulerian force which prevents merging, effectively modelling the presence of surfactants in the system. When the coalescence is inhibited the effective viscosity is always greater than 1 and the curvature of the function representing the emulsion effective viscosity versus the volume fraction becomes positive, resembling the behaviour of suspensions of deformable particles. The reduction of the effective viscosity in the presence of coalescence is associated with the reduction of the total surface of the disperse phase when the droplets merge, which leads to a reduction of the interface tension contribution to the total shear stress. The probability density function of the flow topology parameter shows that the flow is mostly a shear flow in the matrix phase, with regions of extensional flow when the coalescence is prohibited. The flow in the disperse phase, instead, always shows rotational components. The first normal stress difference is positive, except for the smallest viscosity ratio considered, whereas the second normal difference is negative, with their ratio being constant with the volume fraction. Our results clearly show that the coalescence efficiency strongly affects the system rheology and that neglecting droplet merging can lead to erroneous predictions.

Flow over aligned and staggered cube arrays is a classic model problem for rough-wall turbulent boundary layers. Earlier studies of this model problem mainly looked at rough surfaces with a moderate coverage density, i.e. 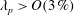$\unicode[STIX]{x1D706}_{p}>O(3\,\%)$, where 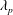$\unicode[STIX]{x1D706}_{p}$ is the surface coverage density and is defined to be the ratio between the area occupied by the roughness and the total ground area. At lower surface coverage densities, i.e. 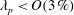$\unicode[STIX]{x1D706}_{p}<O(3\,\%)$, it is conventionally thought that cubical roughness acts like isolated roughness elements; and that the single-cube drag coefficient, i.e. 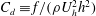$C_{d}\equiv f/(\unicode[STIX]{x1D70C}U_{h}^{2}h^{2})$, equals 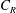$C_{R}$. Here, 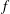$f$ is the drag force on one cubical roughness element, 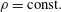$\unicode[STIX]{x1D70C}=\text{const.}$ is the fluid density, 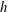$h$ is the height of the cube, 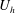$U_{h}$ is the spatially and temporally averaged wind speed at the cube height, and 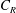$C_{R}$ is the drag coefficient of an isolated cube. In this work, we conduct large-eddy simulations and direct numerical simulations of flow over wall-mounted cubes with very low surface coverage densities, i.e. 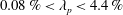$0.08\,\%<\unicode[STIX]{x1D706}_{p}<4.4\,\%$. The large-eddy simulations are at nominally infinite Reynolds numbers. The results challenge the conventional thinking, and we show that, at very low surface coverage densities, the single-cube drag coefficient may increase as a function of 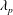$\unicode[STIX]{x1D706}_{p}$. Our analysis suggests that this behaviour may be attributed to secondary turbulent flows. Secondary turbulent flows are often found above spanwise-heterogeneous roughness. Although the roughness considered in this work is nominally homogeneous, the secondary flows in our simulations are very similar to those observed above spanwise-heterogeneous surface roughness. These secondary vortices redistribute the fluid momentum in the outer layer, leading to high-momentum pathways above the wall-mounted cubes and low-momentum pathways at the two sides of the wall-mounted cubes. As a result, the spatially and temporally averaged wind speed at the cube height, i.e. 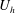$U_{h}$, is an underestimate of the incoming flow to the cubes, which in turn leads to a large drag coefficient 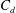$C_{d}$.

An analytical model is developed for the lift force produced by unsteady rotating wings; this configuration is a simple representation of a flapping wing. Modelling this is important for the aerodynamic and control-system design for bio-inspired drones. Such efforts have often been limited to being two-dimensional, semi-empirical, sometimes computationally expensive, or quasi-steady. The current model is unsteady and three-dimensional, yet simple to implement, requiring knowledge of only the wing kinematics and geometry. Rotating wings produce a vortex loop consisting of the root vortex, leading-edge vortex, tip vortex and trailing-edge vortex, which grows with time. This is modelled as a tilted planar loop, geometrically specified by the wing size, orientation and motion. By equating the angular impulse of the vortex loop to that of the fluid volume driven by the wing, the circulatory lift force is derived. Potential flow theory gives the fluid-inertial lift. Adding these two contributions yields the total lift formula. The model shows good agreement with a range of experimental and computational cases. Also, a steady-state lift model is developed that compares well with previous work for various angles of attack.

The work presents an experimental investigation into the motion of and hydrodynamic forces along a single flexible stem in regular waves. The experiment covers a large range in relevant non-dimensional parameters: the drag-to-stiffness ratio $CaL\in [0.003,3.8]$, the inertia-to-stiffness ratio $CaL/KC\in [4\times 10^{-5},14.8]$, the Keulegan–Carpenter number $KC\in [3.8,145]$ and the Reynolds number $Re\in [230,2900]$. The two first parameters relate to the response of the stem in waves and thus account for material properties, while the two last parameters are relevant for hydrodynamic forces on the stem. The displacement of the stem was captured with a digital video camera and the displacement along the stem was captured for every 2.5 mm at 25 Hz. This unique laboratory data set allowed for the following analyses: (i) Determination of the relevant non-dimensional parameter to predict the stem motion and shape. (ii) A direct comparison between the measured force for mimics of two lengths (0.15 m and 0.30 m) illustrating the force reduction potential for flexible mimics. (iii) Direct evaluation of the average force coefficients $C_{D}$ (drag) and $C_{M}$ (inertia) for the flexible stems. (iv) The distributed external hydrodynamic loading and the internal shear forces were estimated from the laboratory experiments. The distribution of the shear force helped to understand the breakage mechanisms of flexible stems. (v) A linkage between phase lags and internal shear forces was suggested. The data set is considered valuable as validation material for numerical models of stem motion in waves.

We study the rheology of a non-colloidal suspension of rigid spherical particles interacting with a viscoelastic matrix. Three-dimensional numerical simulations under shear flow are performed using the smoothed particle hydrodynamics method and compared with experimental data available in the literature using different constant-viscosity elastic Boger fluids. The rheological properties of the Boger matrices are matched in simulation under viscometric flow conditions. Suspension rheology under dilute to semi-concentrated conditions (i.e. up to solid volume fraction $\unicode[STIX]{x1D719}=0.3$) is explored. It is found that at small Deborah numbers $De$ (based on the macroscopic imposed shear rate), relative suspension viscosities $\unicode[STIX]{x1D702}_{r}$ exhibit a plateau at every concentration investigated. By increasing $De$, shear thickening is observed, which is related to the extensional thickening of the underlying viscoelastic matrix. Under dilute conditions ($\unicode[STIX]{x1D719}=0.05$), numerical results for $\unicode[STIX]{x1D702}_{r}$ agree quantitatively with experimental data in both the $De$ and $\unicode[STIX]{x1D719}$ dependences. Even under dilute conditions, simulations of full many-particle systems with no a priori specification of their spatial distribution need to be considered to recover precisely experimental values. By increasing the solid volume fraction towards $\unicode[STIX]{x1D719}=0.3$, despite the fact that the trend is well captured, the agreement remains qualitative with discrepancies arising in the absolute values of $\unicode[STIX]{x1D702}_{r}$ obtained from simulations and experiments but also with large deviations existing among different experiments. With regard to the specific mechanism of elastic thickening, the microstructural analysis shows that elastic thickening correlates well with the average viscoelastic dissipation function $\unicode[STIX]{x1D703}^{elast}$, requiring a scaling as $\langle \unicode[STIX]{x1D703}^{elast}\rangle \sim De^{\unicode[STIX]{x1D6FC}}$ with $\unicode[STIX]{x1D6FC}\geqslant 2$ to take place. Locally, despite the fact that regions of large polymer stretching (and viscoelastic dissipation) can occur everywhere in the domain, flow regions uniquely responsible for the elastic thickening are well correlated to areas with significant extensional component.