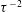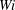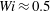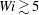We present theoretical, numerical and experimental studies of the release of a finite volume of fluid instantaneously from an edge of a rectangular domain for high Reynolds number flows. For the cases we considered, the results indicate that approximately half of the initial volume exits during an early adjustment period. Then, the inertial gravity current reaches a self-similar phase during which approximately 40 % of its volume drains and its height decreases as $\unicode[STIX]{x1D70F}^{-2}$, where $\unicode[STIX]{x1D70F}$ is a dimensionless time that is derived with the typical gravity wave speed and the horizontal length of the domain. Based on scaling arguments, we reduce the shallow-water partial differential equations into two nonlinear ordinary differential equations (representing the continuity and momentum equations), which are solved analytically by imposing a zero velocity boundary condition at the closed end wall and a critical Froude number condition at the open edge. The solutions are in good agreement with the performed experiments and direct numerical simulations for various geometries, densities and viscosities. This study provides new insights into the dynamical behaviour of a fluid draining from an edge in the inertial regime. The solutions may be useful for environmental, geophysical and engineering applications such as open channel flows, ventilations and dam-break problems.

Thermoacoustic instability is the result of a positive coupling between the acoustic field in the duct and the heat release rate fluctuations from the flame. Recently, in several turbulent combustors, it has been observed that the onset of thermoacoustic instability is preceded by intermittent oscillations, which consist of bursts of periodic oscillations amidst regions of aperiodic oscillations. Quantitative analysis of the intermittency route to thermoacoustic instability has been performed hitherto using the pressure oscillations alone. We perform experiments on a laboratory-scale bluff-body-stabilized turbulent combustor with a backward-facing step at the inlet to obtain simultaneous data of acoustic pressure and heat release rate fluctuations. With this, we show that the onset of thermoacoustic instability is a phenomenon of mutual synchronization between the acoustic pressure and the heat release rate signals, thus emphasizing the importance of the coupling between these non-identical oscillators. We demonstrate that the stable operation corresponds to desynchronized aperiodic oscillations, which, with an increase in the mean velocity of the flow, transition to synchronized periodic oscillations. In between these states, there exists a state of intermittent phase synchronized oscillations, wherein the two oscillators are synchronized during the periodic epochs and desynchronized during the aperiodic epochs of their oscillations. Furthermore, we discover two different types of limit cycle oscillations in our system. We notice a significant increase in the linear correlation between the acoustic pressure and the heat release rate oscillations during the transition from a lower-amplitude limit cycle to a higher-amplitude limit cycle. Further, we present a phenomenological model that qualitatively captures all of the dynamical states of synchronization observed in the experiment. Our analysis shows that the times at which vortices that are shed from the inlet step reach the bluff body play a dominant role in determining the behaviour of the limit cycle oscillations.

In shear flows at transitional Reynolds numbers, localized patches of turbulence, known as puffs, coexist with the laminar flow. Recently, Avila et al. (Phys. Rev. Lett., vol. 110, 2013, 224502) discovered two spatially localized relative periodic solutions for pipe flow, which appeared in a saddle-node bifurcation at low Reynolds number. Combining slicing methods for continuous symmetry reduction with Poincaré sections for the first time in a shear flow setting, we compute and visualize the unstable manifold of the lower-branch solution and show that it extends towards the neighbourhood of the upper-branch solution. Surprisingly, this connection even persists far above the bifurcation point and appears to mediate the first stage of the puff generation: amplification of streamwise localized fluctuations. When the state-space trajectories on the unstable manifold reach the vicinity of the upper branch, corresponding fluctuations expand in space and eventually take the usual shape of a puff.

New variational principles are given for the two-dimensional interactions between gravity-driven water waves and a rotating and translating rectangular vessel dynamically coupled to its interior potential flow with uniform vorticity. The complete set of equations of motion for the exterior water waves, the exact nonlinear hydrodynamic equations of motion for the vessel in the roll/pitch, sway/surge and heave directions, and also the full set of equations of motion for the interior fluid of the vessel, relative to the body coordinate system attached to the rotating–translating vessel, are derived from two Lagrangian functionals.

The stability of an accelerating cylindrical blob of a time-varying radius is considered with the goals of understanding the effects of time dependence of the underlying base state on a Rayleigh–Plateau instability as well as of evaluating a contribution due to a lateral acceleration of the blob, treated as a perturbation here. All of the key processes contributing to instability development are dissected, with analytical analyses of the exact incompressible inviscid potential flow formulation. Herein, without invoking the ‘frozen’ base state assumption, the entire time interval of the evolution of a perturbation is explored, discerning physical mechanisms at each stage of development. It transpires that the stability picture proves to be cardinally different from Rayleigh’s standard analysis.

In this study, we experimentally investigate the turbulent drag-reduction (DR) mechanism in flow through ducts of circular, rectangular and square cross-sections using two grades of polyacrylamide in aqueous solution having different molecular weights and various semidilute concentrations. Specifically, we explore the relationship between drag reduction and fluid elasticity, purposely exploiting the mechanical degradation of polymer molecules to vary their rheological properties. We also obtain time-resolved velocity data for various DR levels using particle image velocimetry and laser Doppler velocimetry. Elasticity is quantified via relaxation times determined from uniaxial extensional flow using a capillary breakup apparatus. A plot of DR against Weissenberg number ($Wi$) is found to approximately collapse the data, with the onset of DR occurring at $Wi\approx 0.5$ and the maximum drag-reduction asymptote being approached for $Wi\gtrsim 5$. Thus quantitative predictions of DR in a range of shear flows can be made from a single measurable material property of a polymer solution, at least for this particular flexible linear polymer.

Pressure- and volume-imposed rheology is used to study suspensions of non-colloidal, rigid fibres in the concentrated regime for aspect ratios ranging from 3 to 15. The suspensions exhibit yield stresses. Subtracting these apparent yield stresses reveals a viscous scaling for both the shear and normal stresses. The variation in aspect ratio does not affect the friction coefficient (ratio of shear and normal stresses), but increasing the aspect ratio lowers the maximum volume fraction at which the suspension flows. Constitutive laws are proposed for the viscosities and the friction coefficient close to the jamming transition.