We report experimental and theoretical results on how a fluid (homogeneous or continuously stratified) is spun up in a closed, semicircular cylinder. Experiments were performed for Rossby numbers 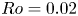 $Ro=0.02$, 0.2 and 1 (the latter corresponding to the limiting case of spin-up from rest), with the Ekman number
$Ro=0.02$, 0.2 and 1 (the latter corresponding to the limiting case of spin-up from rest), with the Ekman number 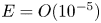 $E=O({10^{-5}})$, and the Burger number (
$E=O({10^{-5}})$, and the Burger number (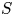 $S$) varied between 0 and 10. There are two key processes: Ekman pumping that drives the core flow; and the formation and breakdown of the vertical-wall boundary layers, with respective characteristic time scales
$S$) varied between 0 and 10. There are two key processes: Ekman pumping that drives the core flow; and the formation and breakdown of the vertical-wall boundary layers, with respective characteristic time scales 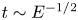 $t\sim E^{-1/2}$ and
$t\sim E^{-1/2}$ and 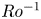 $Ro^{-1}$. When these time scales are comparable, the observed flow is dominated by the gradual spin-up of the initial anticyclone that forms when the rotation rate is increased, which fills the container's interior; vorticity generated adjacent to the vertical walls throughout remains confined to the neighbourhood of the container's walls and corners. Conversely, when
$Ro^{-1}$. When these time scales are comparable, the observed flow is dominated by the gradual spin-up of the initial anticyclone that forms when the rotation rate is increased, which fills the container's interior; vorticity generated adjacent to the vertical walls throughout remains confined to the neighbourhood of the container's walls and corners. Conversely, when 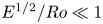 ${E^{1/2}/Ro\ll 1}$, the vertical-wall boundary layers rapidly break down, resulting in the formation of cyclonic vortices in the container's vertical corners, which grow and interact with the initial anticyclone, leading to the formation of a three-cell flow pattern. For
${E^{1/2}/Ro\ll 1}$, the vertical-wall boundary layers rapidly break down, resulting in the formation of cyclonic vortices in the container's vertical corners, which grow and interact with the initial anticyclone, leading to the formation of a three-cell flow pattern. For 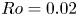 $Ro=0.02$, our theoretical description of the flow generally agrees well with experiments, and the computation of the eruption times for the unsteady boundary layers is consistent with the observations for both
$Ro=0.02$, our theoretical description of the flow generally agrees well with experiments, and the computation of the eruption times for the unsteady boundary layers is consistent with the observations for both 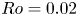 $Ro=0.02$ and
$Ro=0.02$ and  $Ro=0.2$.
$Ro=0.2$.