Using branch continuation in the FENE-P model, we show that finite-amplitude travelling waves borne out of the recently discovered linear instability of viscoelastic channel flow (Khalid et al., J. Fluid Mech., vol. 915, 2021, A43) are substantially subcritical reaching much lower Weissenberg (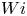 $Wi$) numbers than on the neutral curve at a given Reynolds (
$Wi$) numbers than on the neutral curve at a given Reynolds (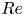 $Re$) number over
$Re$) number over 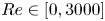 $Re \in [0,3000]$. The travelling waves on the lower branch are surprisingly weak indicating that viscoelastic channel flow is susceptible to (nonlinear) instability triggered by small finite-amplitude disturbances for
$Re \in [0,3000]$. The travelling waves on the lower branch are surprisingly weak indicating that viscoelastic channel flow is susceptible to (nonlinear) instability triggered by small finite-amplitude disturbances for 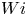 $Wi$ and
$Wi$ and 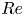 $Re$ well below the neutral curve. The critical
$Re$ well below the neutral curve. The critical 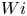 $Wi$ for these waves to appear in a saddle node bifurcation decreases monotonically from, for example,
$Wi$ for these waves to appear in a saddle node bifurcation decreases monotonically from, for example, 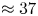 $\approx 37$ at
$\approx 37$ at 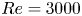 $Re=3000$ down to
$Re=3000$ down to 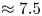 $\approx 7.5$ at
$\approx 7.5$ at 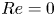 $Re=0$ at the solvent-to-total-viscosity ratio
$Re=0$ at the solvent-to-total-viscosity ratio 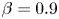 $\beta =0.9$. In this latter creeping flow limit, we also show that these waves exist at
$\beta =0.9$. In this latter creeping flow limit, we also show that these waves exist at 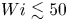 $Wi \lesssim 50$ for higher polymer concentrations,
$Wi \lesssim 50$ for higher polymer concentrations, 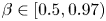 $\beta \in [0.5,0.97)$, where there is no known linear instability. Our results therefore indicate that these travelling waves, found in simulations and named ‘arrowheads’ by Dubief et al. (Phys. Rev. Fluids, vol. 7, 2022, 073301), exist much more generally in
$\beta \in [0.5,0.97)$, where there is no known linear instability. Our results therefore indicate that these travelling waves, found in simulations and named ‘arrowheads’ by Dubief et al. (Phys. Rev. Fluids, vol. 7, 2022, 073301), exist much more generally in 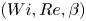 $(Wi,Re, \beta )$ parameter space than their spawning neutral curve and, hence, can either directly, or indirectly through their instabilities, influence the dynamics seen far away from where the flow is linearly unstable. Possible connections to elastic and elasto-inertial turbulence are discussed.
$(Wi,Re, \beta )$ parameter space than their spawning neutral curve and, hence, can either directly, or indirectly through their instabilities, influence the dynamics seen far away from where the flow is linearly unstable. Possible connections to elastic and elasto-inertial turbulence are discussed.