This report is a contribution to the discussion on the solvency problem, which has been taking place at ASTIN-meetings. In his report in Edinburgh 1964 Beard referred to many aspects which are closely connected with the problem. Such aspects are

1. the evaluation of liabilities;

2. the evaluation of assets;

3. the level of the premiums of long term policies and

4. reinsurance.

If all of these are not in order, there is no sense in speaking about solvency. E.g. a solvency margin defined as the difference between assets and the expected value of liabilities would not be a reliable measure of the financial state of an insurance company, if either of these—or maybe both—are not evaluated in a reliable way. The fixing of solvency margins is not an isolated problem, on the contrary it is only part of the security measures which must all be managed at the same time. The ultimate purpose of the security system prescribed by legislation must be to safeguard policyholders and claimants against losses.

This paper deals with some requirements put forward by the Finnish Supervisory Service on technical reserves mainly for solvency reasons. Consequently only one but nevertheless an important aspect of solvency problem is touched upon. The solvency question in its entirety is discussed in a paper of Dr. Pentikainen at this same colloquium.

According to the instructions of the Supervisory Service, given by virtue of the Insurance Companies Act, insurance companies are obliged to calculate a so-called equalisation reserve in a specific way. Simplifying slightly, this equalisation reserve is that part of the technical reserves which exceeds the premium reserve and the claims reserve calculated according to classical actuarial principles; that is to say, the present value of the expectation value of the net insurance liabilities. The Insurance Companies Act calls for this reserve because conventional technical reserves do not take into account the random feature of claims amount.

When experience is insufficient to permit a direct empirical determination of the premium rates of a Stop Loss Cover, we have to fall back upon mathematical models from the theory of probability—especially the collective theory of risk—and upon such assumptions as may be considered reasonable.

The paper deals with some problems connected with such calculations of Stop Loss premiums for a portfolio consisting of non-life insurances. The portfolio was so large that the values of the premium rates and other quantities required could be approximated by their limit values, obtained according to theory when the expected number of claims tends to infinity.

The calculations were based on the following assumptions.

Let F(x, t) denote the probability that the total amount of claims paid during a given period of time is ≤ x when the expected number of claims during the same period increases from o to t. The net premium II (x, t) for a Stop Loss reinsurance covering the amount by which the total amount of claims paid during this period may exceed x, is defined by the formula

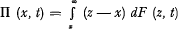
and the variance of the amount (z—x) to be paid on account of the Stop Loss Cover, by the formula

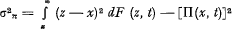
As to the distribution function F(x, t) it is assumed that

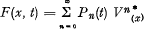
where

Pn(t) is the probability that n claims have occurred during the given period, when the expected number of claims increases from o to t,

V(x) is the distribution function of the claims, giving the conditioned probability that the amount of a claim is ≤ x when it is known that a claim has occurred, and

Vn*(x) is the nth convolution of the function V(x) with itself.

V(x) is supposed to be normalized so that the mean = I.

In this paper an attempt is made to find an answer to the question, “What is the most advantageous size for the retention limit of a risk portfolio, given the fact that a certain stability requirement is to be satisfied?”

This problem will be approached from the viewpoint of an insurer who wishes to obtain a certain degree of stability at lowest cost.

It is assumed that in his choice of reinsurance methods, the insurer restricts himself to either a surplus treaty, a stop loss treaty or a combination of both these types.

Moreover it is assumed that “stability” can be adequately measured by the variance of the risks retained for own account.

We start to consider a reinsurance policy based on the surplus system where the amount of risk in excess of a retention limit u is ceded.

By thus limiting the potential loss on each risk individually, the variance is kept at a certain level, but at the expense of an amount of premium payable to a reinsurer.

The insurer could, of course, reduce the reinsurance cost by increasing his retention but he then is bound to incur a higher variance in his portfolio, which would mean a loss of stability.

One might ask, however, whether a suitably chosen stop loss coverage could bring the variance down again to the proper level at lesser cost than the profit obtained by taking a higher retention. A reduction in reinsurance cost would then have been effected.

The question leads to an optimization problem, which in a more general setting, has been discussed by K. Borch.

Let F(x) be the distribution function of the total amount ξ of claims of an insurance company. It is assumed that this company reduces its liability by means of one or several reinsurance arrangements. Let the remaining part of claims amount be equal to η, which is another random variable. Reinsurance arrangements are supposed to fulfil the following consistency condition: if ξ = x, then almost certainly o ≤ η ≤ x. Presumably all reinsurance arrangements occuring in practice can be supposed to fulfil this requirement.

The problem is to find an optimal reinsurance arrangement, i.e. an optimal random variable η, in the sense that, the net reinsurance premium being given, the variance of η reaches its minimum. In other words, a variable η is looked for, which gives

E{η} = P = const.; V{η} = minimum

In the sequel we use conditional expectations in the sense defined by DOOB ([I]).

Let η be an arbitrary random variable satisfying the consistency condition. If

R(x) = E{η|ξ =x},

then evidently ≤ R(x) ≤ x. Further we have

For the variance the inequality

holds true, since

Clearly the arrangement E {η|ξ} gives also to the reinsurer a smaller variance than the original arrangement.

1.1.— Under Subject 4 at this Congress we have discussed the practical application of modern statistical techniques in different branches of insurance. During the last decades, there has been an almost explosive development in theoretical statistics and related branches of mathematics. I think it has been very useful to survey the techniques, which have been developed, and find out if they can be used in insurance.

1.2. — There may, however, be some danger in this approach. When new means become available, we should of course have an open mind, and examine these means in order to see if they can serve our ends. We should, however, not get so excited over the power of new techniques, that we distort our ends just for the sake of being able to apply the means.

Linear programming, to take an example, is a powerful tool, which has proved extremeiy useful in many, apparently very different fields. There is, however, little point in using this technique in insurance, unless we have problems which consist of determining the maximum of a linear expression, subject to linear restraints. If there are problems in insurance which can be cast in this form, with sufficient approximation, then linear programming is obviously useful. If, however, we lose something essential by reformulating our problems in this way, linear programming may become a dangerous temptation, which we should resist.

It is often found even today in Europe that for certain statistical investigations the conclusion is drawn that the extent of the available statistical data is not sufficient. Going to the root of this pretention, however, we notice that there is a want of clear conception about the extent that is in fact necessary in order that a valid conclusion may with greater probability be arrived at. This, for instance, is the case when obvious tariff reductions are shirked from by entrenching oneself behind the law of large numbers, which by its very nature can in actual practice be never accomplished in its inherent sense.

Apart from a proper understanding of the limits within which a set of statistical data may subject to certain assumptions be ascribed full measure of credence, there is further a lack of the necessary tools that would permit, on the basis of ascertainable values alone, far-reaching conclusions to be drawn or a maximum of useful information to be gathered from an investigation of which the scope is evidently not sufficient.

Credibility Theory, of which Prof. Mowbray [4] may be regarded as the initiator, was evolved in the U.S.A. about 50 years ago to fill this lacunae. The development of Credibility Theory may be considered as one of the most significant contributions of American actuarial science, and it is frankly astonishing that apart from certain specific realisations in the collective risk theory which are fairly closely related to Credibility Theory, it is only in recent years that this interesting topic has met with the required attention in Europe.

Reinsurance forms can roughly be classified into proportional and non-proportional. The authors of this paper had planned to investigate the “efficiency” of two different reinsurance forms, one from each of these categories. Efficiency is here understood as reduction in the variance of the annual results of the risk business achieved per unit of ceded reinsurance risk premium. This investigation may be carried out in full later.

This note will only deal with the interplay between surplus and excess of loss reinsurance; more specifically the effect of changes in the volume of surplus cessions on the excess of loss risk premium.

The study came out of a practical Fire Reinsurance rating problem and will be carried through under very simplified assumptions. Thus we will ignore the conflagration hazard and the possibility of a wrongly taxed PML. This means that if amounts above a PML of M are ceded on a surplus basis the highest loss per event will be M, and an excess cover above a priority m will never pay more than M-m per event.

The following notations will be used

R(M) ceded risk premium volume on surplus basis, the PML retention being M.

πM(m) excess of loss risk premium if priority is m and surplus cessions are made above a PML of M.

Hans Bühlmann traite dans son ouvrage “Optimale Prämien-stufensysteme” (1964) principalement le problème de trouver l'estimation optimale de la prime de la n-ième période à partir des observations de sinistres au cours des périodes précédentes.

Max Gürtler a traité dans le “Bonus ou Malus” du Astin Bulletin vol. III part I deux systèmes différents pour la détermination de la prime individuelle pour l'assurance automobile, c'est-à-dire

a) système “Absence de sinistre”

b) système “Nombre de sinistre”.

A l'aide de simples modèles (examples page 56) pour le groupement de portefeuilles de risques bons et lourds Gürtler étudie l'effet des deux systèmes et en tire des conclusions générales sur l'applicabilité des systèmes. Gürtler souligne d'abord que le système b) utilise considérablement mieux l'information, parce que tous les sinistres y sont considéréd et non pas, comme dans le système a), seulement le premier sinistre étant registré pour chaque assurance.

Marcel Derron traite dans “A theoretical study of the no-claim bonus problem” du même cahier de la publication la quote-part du ER (Error ratio) qu'il définit comme une quote-part égale au montant absolut de la différence entre la prime payée et la vraie prime divisée par la prime payée. Il calcule la quote-part du ER pour le modële de Gürtler et pour des modèles alternatifs et cherche le système de bonification qui rend la quote-part du ER aussi petite que possible pour le modèle choisi.

The relationships between actuarial and pure mathematics are curious. Actuaries have contributed to the development of mathematical theory: it is sufficient to mention, as examples, Fredholm of an earlier, and Cramér of a more recent generation. Scandinavian mathematicians, in particular, have been concerned with a very special type of stochastic process, reflected in the collective theory of risk, and the work of Philipson, Ammeter and others in this field is well known to readers of this Bulletin. However, the main stream of the theory of stochastic processes has little contact with actuarial applications.

On the other hand, many actuaries have studied and assimilated pure mathematics and have thrown light on actuarial matters by describing their own preoccupations in the terminology of modern, often abstract, mathematics. E. Franckx is one of their number.

The Instituto di Matematica Finanziaria of the University of Trieste (Faculty of Economics and Commerce) has published a booklet entitled

Essai d'une théorie opérationnelle des risques Markoviens which contains three lectures delivered by Professor Franckx in Trieste and a contribution which he presented to the 17th Congress of Actuaries, held in London in 1964.

1. In an article on such processes in ASTIN Bull. (II-3, pp. 450–451) the author has derived a relation between cPp i.n.s. (compound Poisson processes in the narrow sense) and composed Poisson processes, which is quite general. In this note this relation shall be simplified under the rather weak condition that Po(t), Pn(t) being the distribution of the number of changes occurring in the interval (o, t), for every fixed value of t, tends to a positive limit less than unity when t tends to infinity.

2. By the theory expounded by Thyrion (Bull, de l'Assoc. Act. Beiges, 1959 and 1963) the characteristic function of the number of events in the interval (o, t) can for each fixed value of t in this case be written

where η is a real variable and i the imaginary unity.

It is easily seen that (1) is equal to the following expression

which has the form of a characteristic function of the number of changes in a composed Poisson process.

1.1. In this paper we shall consider a given portfolio of insurance contracts, and we shall study the following two problems:

(i) How should this portfolio be reinsured?

(ii) What reserves should the company maintain to pay claims which will be made under the contracts in the portfolio?

This means that we shall ignore all questions as to how the company acquired the portfolio, i.e. some of the most important questions concerning management control of insurance companies, such as rating policy, underwriting control etc.

1.2. Even the two simple problems, which are singled out for study in this paper, cannot be solved unless we specify the objectives and the external circumstances of the company.

It is obvious that the reinsurance problem cannot be solved unless we know something about the company's “attitude to risk”, and about the cost of obtaining cover for various kinds of risk in the reinsurance market.

It is also obvious that we cannot solve the reserve problem unless we specify the safety requirements, which the company has to satisfy. We shall see in the following that we may also have to specify the portfolios, which the company expects to underwrite in the future.

This paper was written in connection with the preparation of Marché Commun regulations in the insurance sector and has been submitted to the Commission Technique pour l'étude d'un indice de solvabilité relatif aux entreprises d'assurances contre les dommages. It aims at explaining the scope of the problem to non-mathematicians and for that reason emphasizes its logical in contradistinction to its computational aspects.

The probability of the insurer's ruin has two aspects. The occurrence of the event ruin may be considered with respect to a fixed period but also with respect to a period of undetermined length. In both cases the period starts at a moment at which the insurer's capital (patrimoine) is known and it is intuitively clear that in both cases the probability of ruin will be the higher as the insurer's capital is smaller and the risk to which he is exposed heavier.

For some purposes more precise conclusions are required. This requirement gives rise to problems which will be considered here with respect to the probability of the occurrence of ruin in a period of undetermined length. It will be taken for granted that besides the artificial events occurring in games of chance there are other classes of uncertain events to which numerical probabilities can be assigned and that, as far as claims are concerned, the insurer's losses belong to one of the said classes. On this understanding it makes sense to consider a numerical probability of ruin depending on a fixed initial capital, random losses to which numerical probabilities are assigned, and other profits and losses.