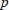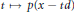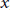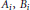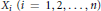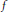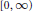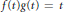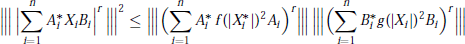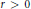We give an affirmative answer to one of the questions posed by Bourin regarding a special type of inequality referred to as subadditivity inequalities in the case of the Hilbert–Schmidt and the trace norms. We formulate the solution for arbitrary commuting positive operators, and we conjecture that it is true for all unitarily invariant norms and all commuting positive operators. New related trace inequalities are also presented.

A homogeneous real polynomial $p$ is hyperbolic with respect to a given vector $d$ if the univariate polynomial $t\,\mapsto \,p(x\,-\,td)$ has all real roots for all vectors $x$. Motivated by partial differential equations, Gårding proved in 1951 that the largest such root is a convex function of $x$, and showed various ways of constructing new hyperbolic polynomials. We present a powerful new such construction, and use it to generalize Gårding’s result to arbitrary symmetric functions of the roots. Many classical and recent inequalities follow easily. We develop various convex-analytic tools for such symmetric functions, of interest in interior-point methods for optimization problems over related cones.

Let 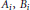${{A}_{i}},\,{{B}_{i}}$ and 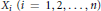${{X}_{i}}\,(i\,=\,1,\,2,\ldots ,\,n)$ be operators on a separable Hilbert space. It is shown that if 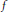$f$ and $g$ are nonnegative continuous functions on 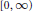$\left[ 0,\infty \right)$ which satisfy the relation 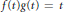$f\,(t)g(t)\,=\,t$ for all $t$ in 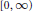$\left[ 0,\infty \right)$, then

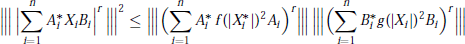$${{\left\| \left| \,{{\left| \sum\limits_{i=1}^{n}{A_{i}^{*}{{X}_{i}}{{B}_{i}}} \right|}^{r}} \right| \right\|}^{2}}\,\le \,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{A_{i}^{*}f{{(\left| X_{i}^{*} \right|)}^{2}}{{A}_{i}}} \right)}^{r}} \right| \right\|\,\,\left\| \left| {{\left( \sum\limits_{i=1}^{n}{B_{i}^{*}g{{(\left| {{X}_{i}} \right|)}^{2}}\,{{B}_{i}}} \right)}^{r}} \right| \right\|$$

for every 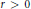$r\,>\,0$ and for every unitarily invariant norm. This result improves some known Cauchy-Schwarz type inequalities. Norm inequalities related to the arithmetic-geometric mean inequality and the classical Heinz inequalities are also obtained.