Liquid bridges are formed when a flowing liquid interacts with multiple parallel fibres, as relevant to heat and mass transfer applications that utilize flow down fibre arrays. We perform a comprehensive experimental study of flowing liquid bridges between two vertical fibres whose spacing is controlled dynamically in our experimental apparatus. The bridge patterns exhibit a regular periodic spacing typical of absolute instability for low flow rates, but become spatially inhomogeneous above a critical flow rate where the base flow is convectively unstable. The shapes of individual bridges and their associated dynamics are measured, as they depend upon the liquid properties, and fibre geometry/spacing. The bridge length scales similarly to static bridges between parallel fibres. The bridge dynamics exhibits a dependence on viscosity and scale with the impedance. A simple energy balance is used to derive a scaling relationship for the bridge velocity that captures the general trend of our experimental data. Finally, we demonstrate that these scalings similarly apply when the fibres are dynamically separated or brought together.

Bistable states for a sufficiently large amount of liquid can appear in an eccentric capillary due to the eccentricity effect under zero gravity (J. Fluid Mech, vol. 863, 2019, pp. 364–385). A transverse body force, which can lead to rich physical phenomena of a droplet, may lead to multistable states (bistability, tristability and the likes) of a sufficiently large amount of liquid in a capillary. We theoretically investigate this situation in a circular or annular capillary tube under a transverse body force. The results show that there can be tristable (bistable) states in an annular (circular) capillary tube: an occluding configuration and two (one) non-occluding configurations. In the annular tube, for one of the non-occluding configurations, the gas–liquid interface in the middle cross-section of the droplet meets both the inner and outer walls of the tube (bridging configuration); for the other non-occluding configuration, the gas–liquid interface in the middle cross-section of the droplet does not meet the inner wall (non-bridging configuration). The multistability is dependent on the Bond number, the contact angle and the cross-sectional shape. The multistability cannot occur for a zero or very large Bond number. A hydrophilic condition (the contact angle smaller than 90°) contributes to the non-occluding non-bridging configuration, while the hydrophobic condition (the contact angle larger than 90°) contributes to the non-occluding bridging configuration (only for the annular capillary). For the annular capillary with a not-so-large contact angle, increasing the inner-to-outer radius ratio can lead to a larger range of Bond numbers, in which the multistability occurs.

When a viscous fluid partially fills a Hele-Shaw channel, and is pushed by a pressure difference, the fluid interface is unstable due to the Saffman–Taylor instability. We consider the evolution of a fluid region of finite extent, bounded between two interfaces, in the limit that the interfaces are close, that is, when the fluid region is a thin liquid filament separating two gases of different pressure. In this limit, we derive a second-order ‘thin-filament’ model that describes the normal velocity of the filament centreline, and evolution of the filament thickness, as functions of the thickness, centreline curvature and their derivatives. We show that the second-order terms in this model, that include the effect of transverse flow along the filament, are necessary to regularise the instability. Numerical simulation of the thin-filament model is shown to be in accordance with level-set computations of the complete two-interface model. Solutions ultimately evolve to form a bubble of rapidly increasing radius and decreasing thickness.

A lattice Boltzmann method is used to explore the effect of surfactants on the unequal volume breakup of a droplet in a T-junction microchannel, and the asymmetry due to fabrication defects in real-life microchannels is modelled as the pressure difference between the two branch outlets ($\Delta {P^\ast }$). We first study the effect of the surfactants on the droplet dynamics at different dimensionless initial droplet lengths ($l_0^\ast $) and capillary numbers (Ca) under symmetric boundary conditions ($\Delta {P^\ast } = 0$). The results indicate that the presence of surfactants promotes droplet deformation and breakup at small and moderate $l_0^\ast $ values, while the surfactant effect is weakened at large $l_0^\ast $ values. When the branch channels are completely blocked by the droplet, a linear relationship is observed between the dimensionless droplet length ($l_d^\ast $) and dimensionless time (${t^\ast }$), and two formulas are proposed for predicting the evolution of $l_d^\ast $ with ${t^\ast }$ for the two systems. We then investigate the effect of the surfactants on the droplet breakup at different values of $\Delta {P^\ast }$ and bulk surfactant concentrations (${\psi _b}$) under asymmetric boundary conditions ($\Delta {P^\ast } \ne 0$). It is observed that, as $\Delta {P^\ast }$ increases, the volume ratio of the generated droplets (${V_1}/{V_2}$) decreases to 0 in both systems, while the rate of decrease is higher in the clean system, i.e. the presence of surfactants could cause a decreased pressure difference between the droplet tips. As ${\psi _b}$ increases, ${V_1}/{V_2}$ first increases rapidly, then remains almost constant and finally decreases slightly. We thus establish a phase diagram that describes the ${V_1}/{V_2}$ variation with $\Delta {P^\ast }$ and ${\psi _b}$.

The linear stability of the axisymmetric steady flow in a thermocapillary liquid bridge made from 2-cSt silicone oil $({Pr}=28)$ is investigated numerically. The liquid bridge is heated either from above or below and exposed to an axial air flow which is confined to a concentric tube surrounding the bridge. At the annular inlet, the air flow is fully developed and has the same temperature as the adjacent support rod. Using an extended Oberbeck–Boussinesq approximation in which the density of both fluids depends linearly on the temperature in all equations, critical thermocapillary Reynolds numbers are obtained depending on the strength of the imposed axial air flow. The critical conditions are sensitive with respect to the direction of a weak air flow, because the air flow changes the plateau value of the interfacial temperature midway between the hot and cold ends. For stronger air flow the critical thermocapillary Reynolds number almost saturates at moderate values. Throughout, the instability arises as a hydrothermal wave with the gas phase being passive. The dynamic interface deformations for axisymmetric flow caused by the thermocapillarity flow in the liquid and by the stresses from the air flow are considered separately. Apart from turning points of the critical curve, the impact of dynamic surface deformations on the critical thermocapillary Reynolds number is moderate.

The axisymmetric steady two-phase flow of a differentially heated thermocapillary liquid bridge in air and its linear stability is investigated numerically, taking into account dynamic interfacial deformations in the basic flow. Since most experiments require a high temperature difference to drive the flow into the three-dimensional regime, the temperature dependence of the material properties must be taken into account. Three different models are investigated for a high-Prandtl-number thermocapillary liquid bridge with nominal Prandtl number ${\textit {Pr}}=28.8$: the Oberbeck–Boussinesq (OB) approximation, a linear temperature dependence of all material properties and a full nonlinear temperature dependence of all material properties. For all models, critical Reynolds numbers are computed as functions of the volume of the liquid bridge, its aspect ratio, its dimensional size and as a function of the strength of a forced axial flow in the ambient air. Under most circumstances the OB approximation overpredicts and the linear model underpredicts the critical Reynolds number, compared with the model based on the full temperature dependence of the material properties. Among the main influence factors are the proper selection of the reference temperature and, at larger temperature differences, the temperature dependence of the viscosity of the liquid.

The presence of thermocapillary (Marangoni) convection in microgravity may help to enhance the heat transfer rate of phase change materials (PCMs) in space applications. We present a three-dimensional numerical investigation of the nonlinear dynamics of a melting PCM placed in a cylindrical container filled with n-octadecane and surrounded by passive air. The heat exchange between the PCM and ambient air is characterized in terms of the Biot number, when the air temperature has a linear profile. The effect of thermocapillary convection on heat transfer and the topology of the melting front is studied by varying the applied temperature difference between the circular supports and the heat transfer through the interface. The evolution of Marangoni convection during the PCM melting leads to the appearance of hydrothermal instabilities. A new mathematical approach for the nonlinear analysis of emerging hydrothermal waves (HTWs) is suggested. Being applied for the first time to the examination of PCMs, this procedure allows us to explore the nature of the coupling between HTWs and heat gain/loss through the interface, and how it changes over time. We observe a variety of dynamics, including standing and travelling waves, and determine their dominant and secondary azimuthal wavenumbers. Coexistence of multiple travelling waves with different wavenumbers, rotating in the same or opposite directions, is among the most fascinating observations.

We demonstrate through the use of a unique acoustically driven microfluidic extensional rheometry platform (ADMiER) that a single measurement – i.e. the time required for a liquid bridge filament comprising a microlitre semen sample to thin and break up under elastocapillary stresses – constitutes an appropriate proxy for quantifying the motile sperm concentration of the sample in place of computer-assisted sperm analysis (CASA) and haemocytometer measurements used in conventional semen assessment – without the need to separately resolve for individual dependencies on each sperm parameter. By benchmarking diagnostic test accuracy results of blind random bull semen samples ($n=35$) against OpenCASA measurements of these parameters, ADMiER is capable of predicting sperm quality to 93.7 % accuracy, 91.4 % sensitivity and 97.5 % specificity, with respect to commonly adopted veterinary industry minimum values for fertility. These results therefore highlight the potential diagnostic capability of the platform as a conceptual first step towards the development of a rapid, low-cost and portable alternative for veterinary male bovine fertility assessment.

We report a molecularly augmented continuum-based computational model of dynamic wetting and apply it to the displacement of an externally driven liquid plug between two partially wetted parallel plates. The results closely follow those obtained in a recent molecular dynamics (MD) study of the same problem (Fernández-Toledano et al., J. Colloid Interface Sci., vol. 587, 2021, pp. 311–323), which we use as a benchmark. We are able to interpret the maximum speed of dewetting $U^*_{{crit}}$ as a fold bifurcation in the steady phase diagram and show that its dependence on the true contact angle $\theta _{{cl}}$ is quantitatively similar to that found using MD. A key feature of the model is that the contact angle is dependent on the speed of the contact line, with $\theta _{{cl}}$ emerging as part of the solution. The model enables us to study the formation of a thin film at dewetting speeds $U^*>U^*_{{crit}}$ across a range of length scales, including those that are computationally prohibitive to MD simulations. We show that the thickness of the film scales linearly with the channel width and is only weakly dependent on the capillary number. This work provides a link between matched asymptotic techniques (valid for larger geometries) and MD simulations (valid for smaller geometries). In addition, we find that the apparent angle, the experimentally visible contact angle at the fold bifurcation, is not zero. This is in contrast to the prediction of conventional treatments based on the lubrication model of flow near the contact line, but consistent with experiment.

When the top of a sessile droplet is contacted by an opposing solid surface, the droplet can transfer depending on the wettabilities and relative velocity of the surfaces. What if the surface receiving the liquid was porous? High-speed imaging was used to capture the transfer of a droplet from a solid substrate to an opposing porous surface. The parameters that were varied include the wettability of the donor substrate, the pore size of the receiving surface and the droplet's volume and working fluid. Generally, the transfer process is split into two sequential regimes, wetting and wicking, with wicking being three orders of magnitude longer than wetting on average. The wetting regime is split into two sub-regimes, the donor-independent and donor-dependent regimes. The donor-independent regime follows the dynamics of droplet coalescence, starting in a mass-limited viscous regime followed by a capillary–inertial regime. The donor-dependent regime is driven by a global change in Laplace pressure across the liquid bridge, with the viscous wedge of the receding contact line being the rate-limiting factor. The wicking regime is governed by Darcy's law, completing the transfer process of the droplet.

The propagation speed, shape and stability of the rim generated by a liquid-curtain breakup are studied. In the experiment, a liquid curtain surrounded by a slot die, edge guides and the surface of a roller breaks at the contact point between the edge guide and roller in a low-Weber-number range, and the rim propagates in the horizontal direction. Except for the initial time, the rim is almost straight and has a nearly constant propagation speed. For an Ohnesorge number much smaller than 1, unevenness occurs on the rim and the droplets separate from it. When the Ohnesorge number is of the order of unity, the rim becomes convex vertically downward, and the liquid lump flows down. The shape, propagation speed and surface stability of the rim are discussed by analysing the equation proposed by Entov & Yarin (J. Fluid Mech., vol. 140, 1984, pp. 91–111). It is shown that the volume flow rate condition at the slot die exit is important to explain the propagation of the rim. Additionally, in the initial stage of the curtain breakup, the Plateau–Rayleigh instability causes unevenness on the rim surface, and after the rim reaches the slot die exit, the Rayleigh–Taylor instability generates a liquid lump on the rim, which grows into droplets when the Ohnesorge number is much less than 1.

The behaviour of a viscous drop squeezed between two horizontal planes (a squeezed Hele-Shaw cell) is treated by both theory and experiment. When the squeezing force 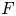$F$ is constant and surface tension is neglected, the theory predicts ultimate growth of the radius 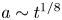$a\sim t^{1/8}$ with time 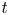$t$. This theory is first reviewed and found to be in excellent agreement with experiment. Surface tension at the drop boundary reduces the interior pressure, and this effect is included in the analysis, although it is negligibly small in the squeezing experiments. An initially elliptic drop tends to become circular as 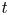$t$ increases. More generally, the circular evolution is found to be stable under small perturbations. If, on the other hand, the force is reversed (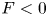$F<0$), so that the plates are drawn apart (the ‘contraction’, or ‘lifting plate’, problem), the boundary of the drop is subject to a fingering instability on a scale determined by surface tension. The effect of a trapped air bubble at the centre of the drop is then considered. The annular evolution of the drop under constant squeezing is still found to follow a ‘one-eighth’ power law, but this is unstable, the instability originating at the boundary of the air bubble, i.e. the inner boundary of the annulus. The air bubble is realised experimentally in two ways: first by simply starting with the drop in the form of an annulus, as nearly circular as possible; and second by forcing four initially separate drops to expand and merge, a process that involves the resolution of ‘contact singularities’ by surface tension. If the plates are drawn apart, the evolution is still subject to the fingering instability driven from the outer boundary of the annulus. This instability is realised experimentally by levering the plates apart at one corner: fingering develops at the outer boundary and spreads rapidly to the interior as the levering is slowly increased. At a later stage, before ultimate rupture of the film and complete separation of the plates, fingering spreads also from the boundary of any interior trapped air bubble, and small cavitation bubbles appear in the very low-pressure region, far from the point of leverage. This exotic behaviour is discussed in the light of the foregoing theoretical analysis.

In this paper we investigate the statics and the dynamics of large-viscosity ligaments attached to a rod and drawn out of a pure-liquid bath. Following the similar work of films pulling out of a bath (Champougny et al., J. Fluid Mech., vol. 811, 2017, pp. 499–524), a one-dimensional model is applied to describe the ligaments drawn at constant velocities. We focus on the whole drawing dynamics of the ligament up to breakup, for which the breakup height is determined. The breakup height coincides with the maximum static meniscus height for very slow drawing, whose process can be described by quasi-static solutions. We present the numerical results of the static menisci and analytically unravel the mechanism in the low gravity case. Starting from a stable static meniscus, the breakup height of faster drawing depends separately on the rod radius and the drawing velocity, the latter dependency being fully determined by considering the agravic limit. Next, it is shown that the entire lifetime of the ligament drawing can be sequenced into a ductility stage, a capillarity stage and a pinch-off stage, the latter being shown to be almost instantaneous. The ductility and capillarity stages are decorrelated with the help of an approximate solution of the ductility stage, and the transition between the two stages corresponds to the time at which the capillarity-induced contraction velocity exceeds the ductility-induced one. The one-dimensional predictions of the breakup height and the entrained liquid volume attached to the rod quantitatively agree with experimental results of silicone oil ligaments, and the deviations are rationalized in comparison with a two-dimensional model.

We study liquid migration in partly saturated shear bands of granular media where liquid is transported away from the shear-band centre. Earlier studies show that the liquid migration can be modelled as a diffusive process with a shear-rate-dependent diffusion coefficient. Here, we apply this model in a two-dimensional Cartesian split-bottom shear cell with one wide, steady shear band. Initially, a high liquid concentration peak develops at the edges of the shear band, which propagates away from the shear band, splitting the shear cell into a liquid-depleted shear-band region and an outer region not yet affected by the liquid migration. Assuming the liquid transport in the vertical direction is negligible, we simplify the liquid migration model to a one-dimensional form evolving over time. By coordinate transformation, an analytically solvable drift-diffusion model is obtained for liquid migration from the simplified model. From here, we obtain analytical solutions for the liquid concentration as a function of space and time. The significance of the mechanisms is studied in terms of the local Péclet number. While drift enhances drying of the shear band and accumulates the liquid in the peak, diffusion shifts the liquid further away from the shear band. To validate the model, we predict numerically the trajectory of the liquid concentration peak from the continuum model and compare with discrete particle method (DPM) simulations. Our continuum model results give a perfect qualitative and an approximate quantitative agreement with the overall results predicted from the DPM model.

In the presence of temperature gradients along the gas–liquid interface, a liquid bridge is prone to hydrothermal instabilities. In the case of a coaxial gas stream, in addition to buoyancy and thermocapillary forces, the shear stresses and interfacial heat transfer affect the development of these instabilities. By combining experimental data with three-dimensional numerical simulations, we examine the evolution of hydrothermal waves in a liquid bridge with $Pr=14$ with a gas flow parallel to the interface. The gas moves from the cold to the hot side with a constant velocity of $0.5\ \textrm {m}\ \textrm {s}^{-1}$ and its temperature is the main control parameter of the study. When the thermal stress ${\rm \Delta} T$ exceeds a critical value ${\rm \Delta} T_{cr}$, a three-dimensional oscillatory flow occurs in the system. A stability window of steady flow has been found to exist in the map of dynamical states in terms of gas temperature and applied thermal stress ${\rm \Delta} T$. The study is carried out by tracking the evolution of hydrothermal waves with increasing gas temperature along three distinct paths with constant values of ${\rm \Delta} T$: path 1 is selected to be just above the threshold of instability while path 2 traverses the stability window and path 3 lies above it. We observe a variety of dynamics including standing and travelling waves, determine their dominant and secondary azimuthal wavenumbers, and suggest the mathematical equations describing hydrothermal waves. Multimodal standing waves, coexistence of travelling waves with several wavenumbers rotating in the same or opposite directions are among the most intriguing observations.

This analysis focuses on the properties of the so-called particle accumulation structures (PAS) in non-cylindrical liquid bridges in normal gravity conditions. In this regard, it follows and integrates the line of inquiry started in Lappa (J. Fluid Mech., vol. 726, 2013, 160) where the main focus was on the effect of high-frequency vibrations. After the discovery (passed almost unnoticed) of a structure (Sasaki et al. Trans. Japan Soc. Mech. Engrs B, vol. 70, 2004) that seems to escape a simple classification on the basis of existing categorizations or paradigms for this type of phenomena, dedicated numerical simulations are carried out in the framework of an integrated Eulerian–Lagrangian approach. Conditions are considered corresponding to isodense and non-isodense particles in a liquid bridge with high aspect ratio, high Prandtl number fluid and hydrostatically deformed interface. Special attention is paid to the very elusive azimuthal wavenumber $m=1$, for which PAS seem to be possible only in a very restricted range of Marangoni numbers. Two distinct families of particle attractors are identified, which coexist in the space of parameters as multiple solutions. We show that the key ingredient needed to unravel the related basins of attraction is the effect of gravity on particles, which may therefore be regarded as an additional mechanism responsible for the formation of these structures in terrestrial liquid bridges.

A long-wave model based on lubrication theory is developed for the flow of a viscous liquid film lining the interior of a tube in the presence of an insoluble surfactant on the interface; no thin-film assumption is made. Linear stability analysis identifies two modes; in the absence of base flow, the ‘interface’ mode is the only unstable mode. The growth rates of this mode serve as an accurate predictor of how surfactant concentration increases plug formation time, and the effects of film thickness on this increase are quantified. In the presence of base flow, both the interface mode and ‘surfactant’ mode may be unstable, resulting in a richer variety of free-surface dynamics. In previous work, turning points in families of travelling wave solutions for a falling viscous film lining the interior of a vertical tube with a clean interface have been shown to be a good indicator of $h_c$, the critical thickness past which plugs may form, and this approach is adapted here for flow with surfactant. It is found that turning points in branches of travelling waves that arise from an unstable surfactant mode give an estimate of $h_c$, provided the interface mode is linearly stable. When both modes are unstable, interpretation of these turning points as they relate to plug formation is more complicated. The study concludes by examining the impact of film thickness on growth rates and travelling wave solutions for core–annular flow with surfactant.

When pushed out of a syringe, polymer solutions form droplets attached by long and slender cylindrical filaments whose diameter decreases exponentially with time before eventually breaking. In the last stages of this process, a striking feature is the self-similarity of the interface shape near the end of the filament. This means that shapes at different times, if properly rescaled, collapse onto a single universal shape. A theoretical description based on the Oldroyd-B model was recently shown to disagree with existing experimental results. By revisiting these measurements and analysing the interface profiles of very diluted polyethylene oxide solutions at high temporal and spatial resolution, we show that they are very well described by the model.

When a viscous liquid bridge between two parallel substrates is stretched by accelerating one substrate, its interface on the plates recedes in the radial direction. In some cases the interface becomes unstable. Such instability leads to the emergence of a network of fingers. In this study, the mechanisms of such fingering are studied experimentally and analysed theoretically. The experimental set-up allows a constant acceleration of a movable substrate at up to 180 m s$^{-2}$. The phenomena are observed using two high-speed video systems. The number of fingers is measured for different liquid viscosities, liquid bridge sizes and wetting conditions. Linear stability analysis of the bridge interface takes into account the inertial, viscous and capillary effects in the liquid flow. The theoretically predicted maximum number of fingers, corresponding to an instability mode with the maximum amplitude, and a threshold for the onset of finger formation are proposed. Both models agree well with the experimental data up to the start of emerging cavitation bubbles.

The experimental study on thermocapillary convection in liquid bridges of large Prandtl number has been carried out on Tiangong-2 in space. The purpose of these experiments is to study the oscillation instability of thermocapillary convection, and to discover and recognize the mechanism of destabilization of thermocapillary convection in the microgravity environment in space. In this paper, the geometry of a half-floating-zone liquid bridge is featured by the aspect ratio Ar and volume ratio Vr, and its influence on critical conditions of oscillatory thermocapillary convection is studied. More than 700 sets of space experiments have been finished. The critical conditions and oscillation characteristics of thermocapillary convection instability in the Ar–Vr parameter space have been fully obtained under microgravity conditions for the first time. It is found that the Ar–Vr parameter space can be divided into two regions of different critical conditions and oscillation characteristics: the region of low frequency oscillation, and the region of high frequency oscillation. More importantly, we obtain the complete configuration of these two stability neutral curves, and find that the low frequency mode is a ‘’ type curve. Based on this, we discuss the influence of heating rate on the oscillation mode. It is found that the heating rate affects the selection of critical mode, which results in a jump change of critical temperature difference. The findings of this study are helpful to better understand the critical modes and transition processes of thermocapillary convection in liquid bridges with different configurations.