If $Y$ is a closed orientable graph manifold, we show that $Y$ admits a coorientable taut foliation if and only if $Y$ is not an L-space. Combined with previous work of Boyer and Clay, this implies that $Y$ is an L-space if and only if $\unicode[STIX]{x1D70B}_{1}(Y)$ is not left-orderable.

We determine the asymptotic behavior of the higher dimensional Reidemeister torsion for the graph manifolds obtained by exceptional surgeries along twist knots. We show that all irreducible $\text{S}{{\text{L}}_{2}}(\mathbb{C})$-representations of the graph manifold are induced by irreducible metabelian representations of the twist knot group. We also give the set of the limits of the leading coeõcients in the higher dimensional Reidemeister torsion explicitly.

We present a graph manifold analog of the Jankins–Neumann classification of Seifert fibered spaces over 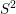$S^{2}$ admitting taut foliations, providing a finite recursive formula to compute the L-space Dehn-filling interval for any graph manifold with torus boundary. As an application of a generalization of this result to Floer simple manifolds, we compute the L-space interval for any cable of a Floer simple knot complement in a closed three-manifold in terms of the original L-space interval, recovering a result of Hedden and Hom as a special case.

An irreducible graph manifold $M$ contains an essential torus if it is not a special Seifert manifold. Whether $M$ contains a closed essential surface of negative Euler characteristic or not depends on the difference of Seifert fibrations from the two sides of a torus system which splits $M$ into Seifert manifolds. However, it is not easy to characterize geometrically the class of irreducible graph manifolds which contain such surfaces. This article studies this problem in the case of graph link exteriors.