The 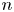 $n$th-order velocity structure function
$n$th-order velocity structure function 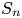 $S_n$ in homogeneous isotropic turbulence is usually represented by
$S_n$ in homogeneous isotropic turbulence is usually represented by 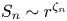 $S_n \sim r^{\zeta _n}$, where the spatial separation
$S_n \sim r^{\zeta _n}$, where the spatial separation 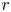 $r$ lies within the inertial range. The first prediction for
$r$ lies within the inertial range. The first prediction for  $\zeta _n$ (i.e.
$\zeta _n$ (i.e. 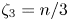 $\zeta _3=n/3$) was proposed by Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941) using a dimensional argument. Subsequently, starting with Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85), models for the intermittency of the turbulent energy dissipation have predicted values of
$\zeta _3=n/3$) was proposed by Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941) using a dimensional argument. Subsequently, starting with Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85), models for the intermittency of the turbulent energy dissipation have predicted values of 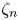 $\zeta _n$ that, except for
$\zeta _n$ that, except for 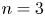 $n=3$, differ from
$n=3$, differ from 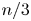 $n/3$. In order to assess differences between predictions of
$n/3$. In order to assess differences between predictions of 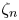 $\zeta _n$, we use the Hölder inequality to derive exact relations, denoted plausibility constraints. We first derive the constraint
$\zeta _n$, we use the Hölder inequality to derive exact relations, denoted plausibility constraints. We first derive the constraint 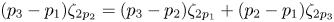 $(p_3-p_1)\zeta _{2p_2} = (p_3 -p_2)\zeta _{2p_1} +(p_2-p_1)\zeta _{2p_3}$ between the exponents
$(p_3-p_1)\zeta _{2p_2} = (p_3 -p_2)\zeta _{2p_1} +(p_2-p_1)\zeta _{2p_3}$ between the exponents 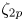 $\zeta _{2p}$, where
$\zeta _{2p}$, where 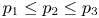 $p_1 \leq p_2 \leq p_3$ are any three positive numbers. It is further shown that this relation leads to
$p_1 \leq p_2 \leq p_3$ are any three positive numbers. It is further shown that this relation leads to  $\zeta _{2p} = p \zeta _2$. It is also shown that the relation
$\zeta _{2p} = p \zeta _2$. It is also shown that the relation  $\zeta _n=n/3$, which complies with
$\zeta _n=n/3$, which complies with  $\zeta _{2p} = p \zeta _2$, can be derived from constraints imposed on
$\zeta _{2p} = p \zeta _2$, can be derived from constraints imposed on 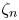 $\zeta _n$ using the Cauchy–Schwarz inequality, a special case of the Hölder inequality. These results show that while the intermittency of
$\zeta _n$ using the Cauchy–Schwarz inequality, a special case of the Hölder inequality. These results show that while the intermittency of 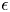 $\epsilon$, which is not ignored in the present analysis, is not incompatible with the plausible relation
$\epsilon$, which is not ignored in the present analysis, is not incompatible with the plausible relation 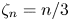 $\zeta _n=n/3$, the prediction
$\zeta _n=n/3$, the prediction 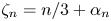 $\zeta _n=n/3 +\alpha _n$ is not plausible, unless
$\zeta _n=n/3 +\alpha _n$ is not plausible, unless 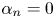 $\alpha _n =0$.
$\alpha _n =0$.