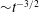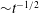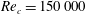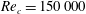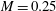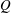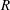Discrete unstable modes of hypersonic laminar boundary layers, obtained from an eigenvalue analysis, provide insight into key transition scenarios. The character of such modes near the leading edge is often identified with the corresponding asymptotic free-stream behaviour of acoustic, vortical or entropic (thermal) content, which we designate fluid-thermodynamic (FT) components. In downstream regions, however, this direct one-to-one correspondence between discrete modes and FT components does not hold, since FT components interact in well-defined ways with the basic state and with each other (even under linear scenarios). In the present work, we perform an FT decomposition of discrete modes using momentum potential theory, to yield a physics-based analysis that complements linear stability theory in the linear regime, and seamlessly extends to the nonlinear domain where direct numerical simulations are appropriate. Linear and nonlinear saturated disturbance effects, different forcing types and wall thermal conditions are considered, with emphasis on phenomena occurring near stability-mode synchronization locations. The results show that, in the linear regime, each discrete mode contains all FT components, whose relative amplitudes vary with streamwise distance. Vortical components are always the largest, followed by thermal and acoustic components. These latter two show distinct fore and aft signatures near mode synchronization. The vortical component displays a series of rope-shaped recirculation-cell patterns across the generalized inflection point. However, both acoustic and thermal components display ‘trapped’ structures. The former contains an alternating monopole array between the wall and the critical layer, while the latter is confined to an undulating region between the wall and a wavy locus straddling the generalized inflection point. Nonlinear saturation in the region of Mack-mode growth further strengthens the rope-shaped structures in the vortical component and higher harmonics appear, whose form and location depend on the specific component. Wall cooling modifies the eigenfunctions such that the acoustic component accounts for more of its composition, consistent with its destabilization. Analysis of energy interactions among the FT components indicates that, even though the vorticity component is the largest, the thermal component induces the most significant source term for the growth of acoustic perturbations, possibly due to the trapped nature of both.
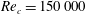 $Re_{c}=150\,000$
$Re_{c}=150\,000$